Знакочередующиеся ряды. Теорема Лейбница

Будем теперь рассматривать ряды, члены которых имеют чередующиеся знаки, т.е. ряды вида

где положительны.

Теорема. Если в знакочередующемся ряде

члены таковы, что

и

то ряд сходится, его сумма положительна и не превосходит первого члена.

Доказательство. Рассмотрим сумму первых членов ряда

Из условия следует, что выражение в каждой скобке положительно. Следовательно, сумма положительна, и возрастает с возрастанием Запишем теперь эту же сумму так:

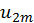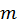В силу условия каждая из скобок положительна. Поэтому в результате вычитания этих скобок и из мы получим число, меньшее, чем т.е. Таким образом, мы установили, что при возрастании возрастает и ограничена сверху. Отсюда следует, что имеет предел причем Однако, сходимость ряда еще не доказана; мы доказали только, что последовательность 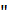четных 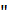частичных сумм имеет пределом число 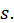Докажем теперь, что 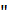нечетные 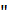частичные суммы также стремятся к пределу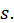

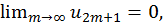Так как по условию то, следовательно,

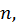Тем самым мы доказали, что как при четном так и при нечетном 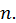Следовательно, ряд сходится.

Замечание 1. Теорема Лейбница справедлива, если неравенства выполняются, начиная с некоторого

Замечание 2. Если знакочередующийся ряд удовлетворяет условию теоремы Лейбница, то нетрудно оценить ошибку, которая получится, если заменить его сумму частичной суммой При такой замене мы отбрасываем все члены ряда, начиная с Но эти числа сами образуют знакочередующийся ряд, сумма которого по абсолютной величине меньше первого члена этого ряда (т.е. меньше Значит, ошибка, совершаемая при замене 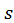на не превосходит по абсолютной величине первого из отброшенных членов.

Пример.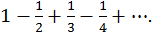

Этот ряд сходится, так как

1)

2)

Сумма первых членов отличается от суммы ряда на величину меньшую, чем

Поиск по сайту: