Теорема Коши об отношении конечных приращений двух функций

Если 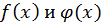- две дифференцируемые на 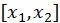функции, причем 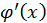нигде внутри отрезка не обращается в нуль, то внутри отрезка 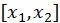найдется такая точка что

(2)

Доказательство. Определим число равенеством:

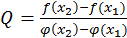(3)

Отметим, что т.к. в противном случае равнялось бы и тогда по теореме Ролля производная обращалась бы в нуль внутри отрезка, что противоречит условию теоремы. Составим вспомогательную функцию

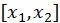Заметив, что функция на отрезке удовлетворяет всем условиям теоремы Ролля, заключаем, что существует такое значение что Но следовательно,

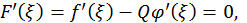откуда Подставляя значение в (3), получим (2).

Замечание. Теорему Коши нельзя доказать, как это может показаться с первого взгляда, применением теоремы Лагранжа к числителю и знаменателю дроби: . Действительно, мы получили бы в этом случае (после сокращения на формулу

в которой Но так как, вообще говоря, 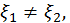то полученный результат, очевидно, не дает еще теоремы Коши.

Раскрытие неопределенностей вида Правило Лопиталя

Пусть функции на некотором отрезке удовлетворяют условиям теоремы Коши и обращаются в нуль в точке этого отрезка, т.е. Отношение не определено при но имеет вполне определенный смысл при значениях Следовательно, может быть поставлен вопрос о разыскании предела этого отношения при Вычисление пределов такого типа называется обычно “раскрытием неопределенностей вида 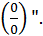С такого рода задачей мы уже имели дело и раньше, например, при рассмотрении предела Выражение при не имеет смысла, но мы видели, что предел при существует и равняется 1.

Теорема. (Правило Лопиталя). Пусть функции на некотором отрезке удовлетворяют условиям теоремы Коши и обращаются в нуль в точке т.е. 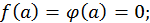тогда, если существует предел отношения при то существует и причем

Доказательство. Возьмем на отрезке какую-нибудь точку Применяя формулу Коши, будем иметь где ξ лежит между Но по условию 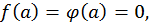значит Если то и Поэтому

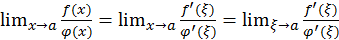= и окончательно

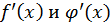Если и производные удовлетворяют тем условиям, которые были наложены в условиях теоремы на функции и то применяя правило Лопиталя к отношению приходим к формуле и т.д.

В правиле Лопиталя может быть как конечным числом, так и ∞.

Замечание. Правило Лопиталя можно применять и при раскрытии неопределенностей вида .(Примем это без доказательства).

Раскрытие неопределенностей вида

1) Пусть 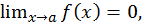требуется найти Это – неопределенность типа

Если искомое выражение переписать в виде или то при мы получим неопределенность или

2) Пусть требуется найти Это – неопределенность типа 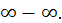Преобразуем и раскроем сначала неопределенность (вида если то следует привести выражение к виду (неопределенность

3) Неопределенности видов 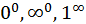раскрываются с помощью предварительного логарифмирования. Эти неопределенности сводятся к случаю неопределенности

Например, пусть 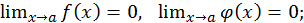требуется найти Это – неопределенность вида Положив прологарифмируем обе части полученного равенства: При получим (справа) неопределенность вида Найдя легко получить Действительно, в силу непрерывности логарифмической функции, 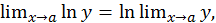и если то, очевидно,

Аналогичным приемом раскрываются и неопределенности видов: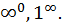

В некоторых случаях правило Лопиталя полезно комбинировать с нахождением пределов элементарными способами.

Лекция 2

Поиск по сайту: