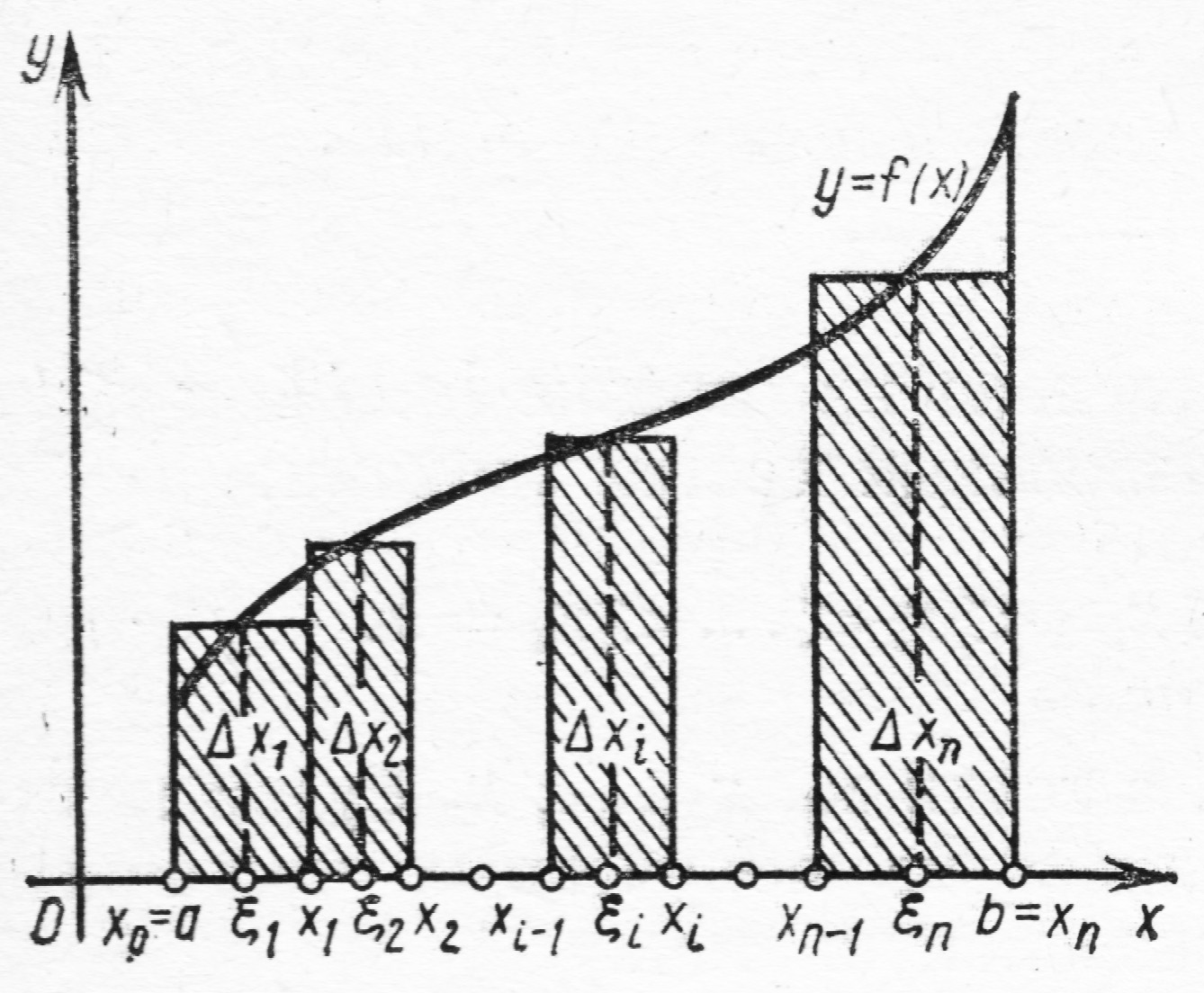
Задача о площади криволинейной трапеции

Пусть на задана непрерывная функция 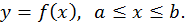Попытаемся вычислить площадь криволинейной трапеции – фигуры, ограниченной сверху графиком функции 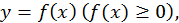слева и справа – отрезками прямых и 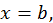снизу – осью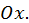

Разобьем произвольным образом при помощи некоторых несовпадающих друг с другом точек

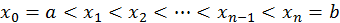на элементарных отрезков

длины которых обозначим через

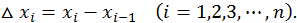
Проведем ординаты, соответствующие точкам деления, тогда криволинейная трапеция разобьется на ряд полосок. В каждом из элементарных отрезков выберем произвольно точку и вычислим в ней значение данной функции 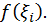Произведение 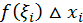выражает площадь прямоугольника с основанием 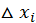и высотой 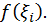Составим сумму всех таких произведений

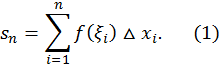
Эта сумма называется интегральной суммой (или суммой Римана) для функции на отрезке Она выражает площадь ступенчатой фигуры, состоящей из прямоугольников и приближенно заменяющей данную трапецию. Очевидно, интегральная сумма (1) зависит от способа разбиения и выбора точек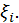

Введем понятие предела интегральной суммы. Число называется пределом интегральной суммы (1) при если 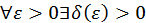такое, что 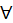для любого разбиения из 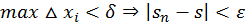независимо от выбора точек на отрезках

Предположим, что рассматриваемая сумма имеет предел, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю; этот предел дает площадь криволинейной трапеции и называется определенным интегралом от функции 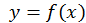на отрезке Обозначение

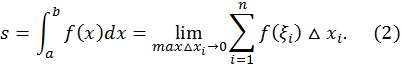
называется подынтегральной функцией, 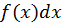– подынтегральным выражением, - переменной интегрирования, - нижним пределом интегрирования, 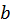- верхним пределом интегрирования.

Из определения следует, что величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.

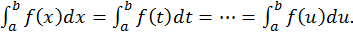
Функция, для которой существует предел (2), называется интегрируемой на отрезке

Из рассмотренной задачи становится ясным геометрический смысл определенного интеграла – он равен площади соответствующей криволинейной трапеции.

Поиск по сайту: