Длина дуги кривой в полярных координатах

Пусть в полярных координатах задано уравнение кривой где полярный радиус, полярный угол

Напишем формулы перехода от полярных координат к прямоугольным

Если сюда вместо подставим его выражение через то получим уравнения Эти уравнения можно рассматривать как параметрические уравнения кривой и для вычисления длины дуги применим формулу (8). Для этого найдем

Тогда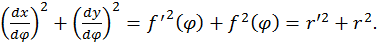

Следовательно,

Вычисление объема тела по площадям параллельных сечений

Пусть имеем некоторое тело. Предположим, что известна площадь любого сечения этого тела плоскостью, перпендикулярной к оси 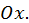Эта площадь будет зависеть от положения секущей плоскости, т.е. будет функцией от Предположим, что непрерывная функция, а также, что все тело заключено между двумя перпендикулярными к оси плоскостями, пересекающими ее в точках и Разобьем произвольным образом тело на слоев с помощью секущих плоскостей, перпендикулярных к оси и пересекающих ее в точках В каждом частичном промежутке 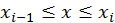выберем произвольную точку 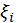и для каждого значения 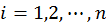построим цилиндрическое тело, образующая которого параллельна оси а направляющая представляет собой контур сечения тела плоскостью Объем такого элементарного цилиндра с площадью основания и высотой равен Объем всех цилиндров будет: 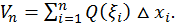Предел этой суммы при (если он существует) называется объемом данного тела:

Пример. Вычислить объем трехосного эллипсоида:

В сечении эллипсоида плоскостью, параллельной плоскости и отстоящей на расстоянии от нее, получится эллипс:

c полуосями .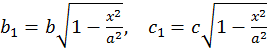

Но площадь такого эллипса равняется

Поэтому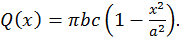

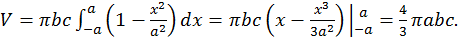
В частности, если 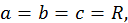эллипсоид превращается в шар, и

Объем тела вращения

Рассмотрим тело, образованное вращением вокруг оси криволинейной трапеции В этом случае Применяя общую формулу 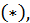получим формулу для вычисления объема тела вращения:

Аналогично можно получить формулу для вычисления объема тела, образованного вращением вокруг оси криволинейной трапеции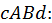

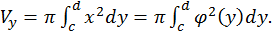
Лекция 18.

Поиск по сайту: