Нахождение наибольшего и наименьшего значений

Теорема. Функция нескольких переменных, непрерывная в ограниченной и замкнутой области, достигает в этой области своего наименьшего и наибольшего значений либо в критических точках функции, принадлежащих этой области, либо в граничных точках области. (Без доказательства).

Для нахождения наибольшего и наименьшего значений функции в замкнутой ограниченной области необходимо:

1. Найти критические точки (лежащие внутри данной области) и вычислить в них значения функции. При этом нет необходимости исследовать функцию на экстремум с помощью частных производных второго порядка.

2. Найти наибольшее и наименьшее значения функции на границе области. Для функции 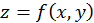граница состоит из нескольких дуг или отрезков, уравнения которых где или где поэтому на соответствующих дугах или отрезках границы данная функция является функцией одной переменной: или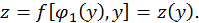

Если граница задана параметрическими уравнениями:

то данная функция также превращается в функцию одной переменной:

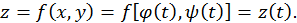
Итак, нахождение наибольшего и наименьшего значений на границе области для функции двух переменных сводится к нахождению наибольшего и наименьшего значений функции одной переменной на отрезке.

3. Сравнить все значения функции: самое большое будет наибольшим значением функции в данной области, самое маленькое – наименьшим.

Поиск по сайту: