Замена переменного в определенном интеграле

Теорема. Пусть дан интеграл где функция непрерывна на отрезке Введем новое переменное по формуле

Если 1)

2) 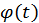и непрерывны на отрезке

3) определена и непрерывна на отрезке то

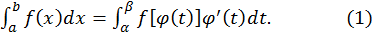
Доказательство. Если 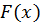есть первообразная для функции 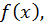то можем написать следующие равенства:

Из (2) получаем:

Из (3) получаем:

Правые части последних выражений равны, следовательно, равны и левые.

Замечание. При вычислении определенного интеграла по формуле (1) мы не возвращаемся к старой переменной. Если мы вычислим второй из определенных интегралов равенства (1), то мы получим некоторое число; этому же числу равняется и первый интеграл.

Пример.

Сделаем подстановку:

Определим новые пределы:

	0	R
	0

Следовательно,

Вычисленный интеграл с геометрической точки зрения представляет площадь круга, ограниченного окружностью

Поиск по сайту: