Формула Тейлора. Формула, которую мы сегодня получим, является одной из основных формул математического анализа и имеет многочисленные приложения как в анализе

Формула, которую мы сегодня получим, является одной из основных формул математического анализа и имеет многочисленные приложения как в анализе, так и в смежных дисциплинах.

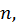Предположим, что функция имеет все производные до порядка включительно в некотором промежутке, содержащем точку Найдем многочлен степени не выше значение которого в точке равняется значению функции в этой точке, а значения его производных до порядка в точке равняются значениям соответствующих производных от функции в этой точке.

Естественно ожидать, что такой многочлен в некотором смысле “близок” к функции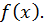

Будем искать этот многочлен в форме многочлена по степеням 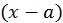с неопределенными коэффициентами.

Неопределенные коэффициенты определим так, чтобы удовлетворялись условия (1).

Предварительно найдем производные от

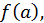
Подставляя в левые и правые части равенств (2) и (3) вместо значение и заменяя на основании равенств (1) через через и т.д., получим:

откуда находим

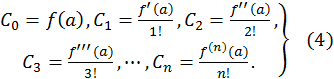
Подставляя найденные значения в (2), получим:

Обозначим через разность значений данной функции и построенного многочлена тогда будем иметь:

называется остаточным членом. Для тех значений для которых остаточный член мал, многочлен дает приближенное представление функции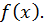

Остаточный член обычно записывают в так называемой форме Лагранжа: , где

Подставив (5) и (7) в (6), получим формулу Тейлора для функции с остаточным членом в форме Лагранжа:

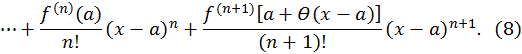
Если в формуле Тейлора положить то получим формулу Маклорена:

Поиск по сайту: