Интегрирование рациональных функций

Рациональные функции бывают целыми (многочлены) и дробными (отношение двух многочленов).

Неопределенный интеграл от целой рациональной функции (многочлена) находится непосредственно:

Дробную рациональную функцию (рациональную дробь) будем задавать так:

Не ограничивая общности рассуждения, будем предполагать, что эти многочлены не имеют общих корней. Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной. Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:

здесь многочлен, а 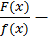правильная дробь.

Так как интегрирование многочленов не представляет затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей.

Существует четыре типа простейших правильных рациональных дробей:

1.

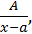
2. ( целое положительное число ),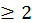

3. (корни знаменателя комплексные, т.е.

4. ( целое положительное число

Всякую правильную рациональную дробь можно представить в виде суммы простейших правильных рациональных дробей. Поэтому мы рассмотрим сначала интегралы от простейших дробей.

Интегрирование простейших дробей типа 1, 2 и 3 не представляет большой трудности.

1.

2.

3.

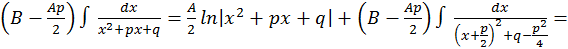
Более сложных вычислений требует интегрирование простейших дробей 4 типа.

4.

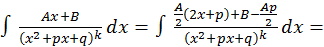
Первый интеграл вычисляется просто:

Второй интеграл обозначим 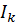и вычислим отдельно:

Обозначим

(корни знаменателя комплексные, следовательно,

Здесь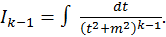

Возьмем последний интеграл в формуле (1) по частям:

Подставляя в (1), получим:

Это так называемая рекуррентная формула.

Сначала находим .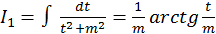

Затем, подставляя в рекуррентную формулу , находим Далее, подставляя в рекуррентную формулу находим Продолжая этот процесс, находим для любого целого положительного

Лекция 12.

Поиск по сайту: