 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Знакопеременные ряды. Абсолютная и условная сходимость
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные. Рассмотренные только что знакочередующиеся ряды являются, очевидно, частным случаем знакопеременных рядов. Здесь будем полагать, что  могут быть как положительными, так и отрицательными.
могут быть как положительными, так и отрицательными.
Следующая теорема дает важный достаточный признак сходимости знакопеременного ряда.
Теорема 1. Если знакопеременный ряд

таков, что ряд, составленный из абсолютных величин его членов
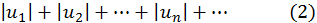
сходится, то и данный знакопеременный ряд также сходится.
Доказательство. Пусть  и
и 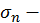 суммы
суммы  первых членов рядов
первых членов рядов  и
и  Пусть далее
Пусть далее  сумма всех положительных, а
сумма всех положительных, а  сумма абсолютных величин всех отрицательных членов среди первых
сумма абсолютных величин всех отрицательных членов среди первых  членов данного ряда; тогда
членов данного ряда; тогда 
По условию, 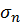 имеет предел
имеет предел 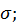
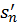 и
и  положительные возрастающие величины, меньшие
положительные возрастающие величины, меньшие 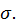 Следовательно, они имеют пределы
Следовательно, они имеют пределы 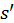 и
и 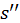 . Из соотношения
. Из соотношения 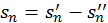 следует, что и
следует, что и  имеет предел и этот предел равен
имеет предел и этот предел равен  т.е. знакопеременный ряд
т.е. знакопеременный ряд  сходится.
сходится.
Доказанная теорема дает возможность судить о сходимости некоторых знакопеременных рядов.
Пример. Исследовать сходимость ряда

где 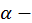 любое число.
любое число.
Наряду с 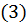 , рассмотрим ряды
, рассмотрим ряды


Ряд  сходится (доказывается с помощью интегрального признака Коши:
сходится (доказывается с помощью интегрального признака Коши:  Члены ряда
Члены ряда 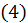 не больше соответственных членов ряда
не больше соответственных членов ряда  следовательно, ряд
следовательно, ряд 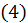 тоже сходится. Но тогда, в силу доказанной теоремы,
тоже сходится. Но тогда, в силу доказанной теоремы, 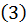 тоже сходится.
тоже сходится.
Признак сходимости, доказанный выше, является только достаточным признаком сходимости знакопеременного ряда, но не необходимым: существуют такие знакопеременные ряды, которые сами сходятся, но ряды, составленные из абсолютных величин их членов, расходятся. В связи с этим полезно ввести понятия об абсолютной и условной сходимости знакопеременного ряда и на основе этих понятий классифицировать знакопеременные ряды.
Знакопеременный ряд  называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов  . Если же знакопеременный ряд
. Если же знакопеременный ряд  сходится, а ряд
сходится, а ряд 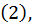 составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд
составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд  называется условно или неабсолютно сходящимся рядом.
называется условно или неабсолютно сходящимся рядом.
В заключение отметим без доказательства следующие свойства абсолютно сходящихся и условно сходящихся рядов.
Теорема 2. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
Теорема 3. Если ряд сходится условно, то какое бы мы ни задали число  можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной
можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной  Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки, окажется расходящимся.
Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки, окажется расходящимся.
Пример 1. В знакопеременных рядах нельзя даже группировать члены. Знакомый нам ряд 
является расходящимся. После группировки членов

Получаем сходящийся ряд, его сумма равна нулю.
При другой группировке членов
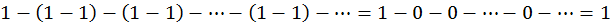
получаем сходящийся ряд, сумма которого равна единице.
Пример 2. Знакопеременный ряд 
является условно сходящимся. Обозначим его сумму через 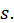 Очевидно, что
Очевидно, что  Сделаем перестановку его членов так, чтобы за одним положительным членом следовали два отрицательных:
Сделаем перестановку его членов так, чтобы за одним положительным членом следовали два отрицательных:
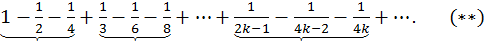
Докажем, что полученный ряд сходится, но что его сумма 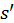 в два раза меньше суммы ряда
в два раза меньше суммы ряда 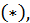 т.е. равна
т.е. равна  Обозначим через
Обозначим через  и
и 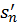 частичные суммы рядов
частичные суммы рядов  и
и 
Рассмотрим сумму  членов ряда
членов ряда 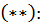




Следовательно,

Далее,
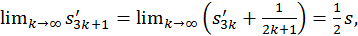
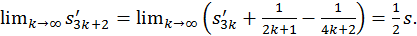
Таким образом, получаем

Итак, в данном случае сумма ряда изменилась после перестановки его членов (уменьшилась вдвое).
Лекция 22.
Поиск по сайту: