 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема о необходимом условии экстремума функции
В точке экстремума дифференцируемой функции производная этой функции равна нулю.
Доказательство. Пусть для определенности 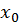 есть точка минимума функции
есть точка минимума функции 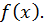 Следовательно,
Следовательно, 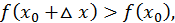 если
если  достаточно мало по абсолютной величине. Отсюда
достаточно мало по абсолютной величине. Отсюда
 если
если  ,
,
 если
если 
Переходя в этих неравенствах к пределу при  получим
получим
 если
если 
 если
если 
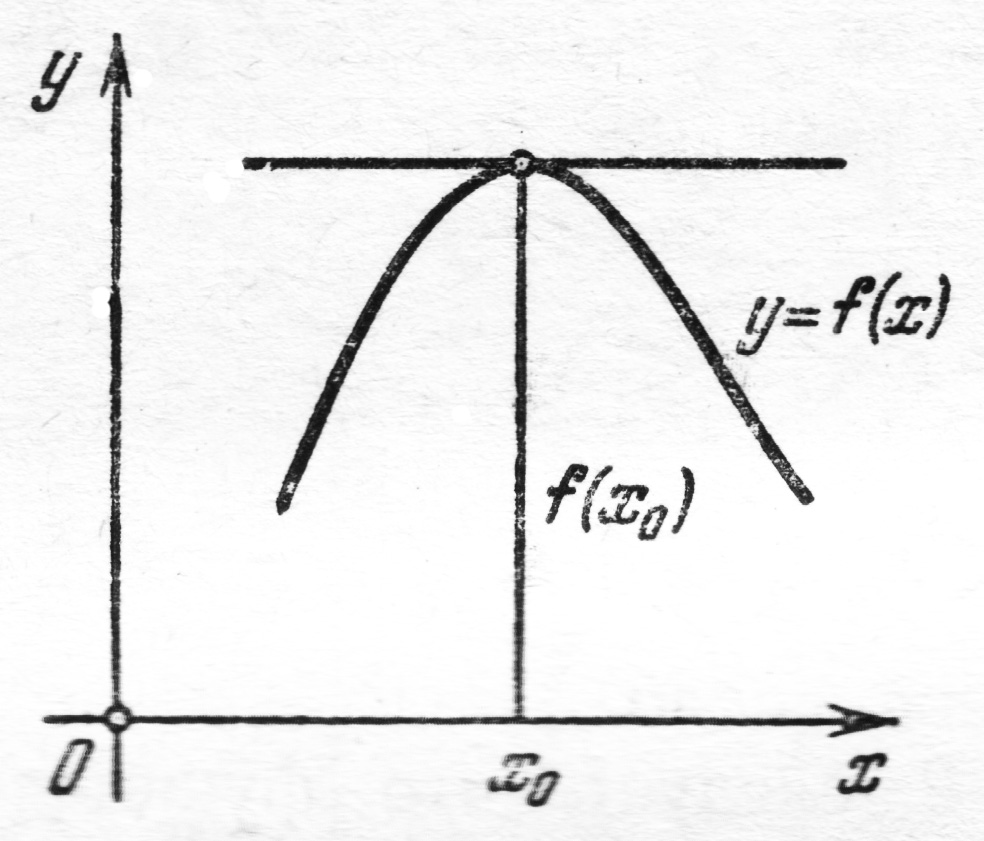 Так как значение производной
Так как значение производной  не должно зависеть от способа стремления
не должно зависеть от способа стремления  к нулю, то отсюда следует, что
к нулю, то отсюда следует, что  Теорема доказана. Аналогичным образом теорема доказывается и для случая максимума функции (доказать самим).
Теорема доказана. Аналогичным образом теорема доказывается и для случая максимума функции (доказать самим).
Геометрически условие 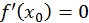 обозначает, что в точке
обозначает, что в точке 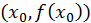
касательная к графику функции  параллельна оси
параллельна оси 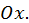
Следствие из теоремы.
Если при всех рассматриваемых значениях аргумента  функция
функция  имеет производную, то она может иметь экстремум только при тех значениях, при которых производная обращается в нуль.
имеет производную, то она может иметь экстремум только при тех значениях, при которых производная обращается в нуль.
 Обратное заключение неверно: не при всяком значении, при котором производная обращается в нуль, обязательно существует экстремум. Например, функция
Обратное заключение неверно: не при всяком значении, при котором производная обращается в нуль, обязательно существует экстремум. Например, функция 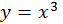 при
при  имеет производную, равную нулю:
имеет производную, равную нулю: 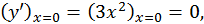 но в этой точке функция не имеет экстремума
но в этой точке функция не имеет экстремума 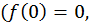


Мы исследовали случай, когда функция во всех точках некоторого отрезка имеет производную. Покажем сейчас на примерах, что в точках, где производная не существует, может быть или максимум, или минимум, но может и не быть ни того, ни другого.
 Пример 1. Функция
Пример 1. Функция  не имеет производной в точке
не имеет производной в точке  но в этой точке данная функция имеет минимум:
но в этой точке данная функция имеет минимум:  тогда как для всякой точки
тогда как для всякой точки  отличной от нуля, имеем
отличной от нуля, имеем 
 Пример 2. Функция
Пример 2. Функция  не имеет производной при
не имеет производной при 
 В этой точке функция не имеет ни максимума, ни минимума:
В этой точке функция не имеет ни максимума, ни минимума: 


Таким образом функция может иметь экстремум лишь в двух случаях: либо в тех точках, где производная существует и равна нулю; либо в тех точках, где производная не существует.
Те значения аргумента  которые для данной функции
которые для данной функции  обращают в нуль ее производную
обращают в нуль ее производную 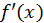 или для которых производная
или для которых производная 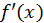 не существует, называются критическими значениями аргумента или критическими точками первого рода.
не существует, называются критическими значениями аргумента или критическими точками первого рода.
Поиск по сайту: