Несобственные интегралы

При введении определенного интеграла 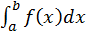предполагалось, что выполняются условия:

1) пределы интегрирования и являются конечными;

2) подынтегральная функция непрерывна на

Если эти оба условия выполняются, то такой интеграл называется собственным определенным интегралом. Но слово собственный обычно опускается.

Если хотя бы одно из двух указанных условий не выполняется, то интеграл называется несобственным определенным интегралом. Слово определенный здесь обычно опускается.

Мы будем изучать несобственные интегралы двух видов:

1.Интегралы с бесконечными пределами (когда нарушается условие 1)).

2.Интегралы от разрывных функций (когда нарушается условие 2)).

Поиск по сайту: