Теорема о достаточном условии вогнутости (выпуклости) графика функции

1) Если для дважды дифференцируемой функции 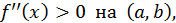то график этой функции будет вогнутым в данном промежутке.

2) Если же то график функции будет выпуклым в этом промежутке.

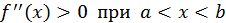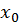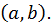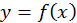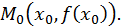Доказательство. 1) Пусть и - любая точка Сравним в точке ординату кривой с ординатой ее касательной проведенной в точке Так как угловой коэффициент касательной равен то 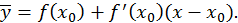Отсюда 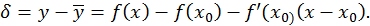Используя теорему Лагранжа, будем иметь 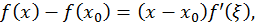где - точка, лежащая между Поэтому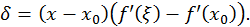

Так как 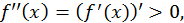то 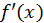- возрастающая функция.

Пусть ; тогда 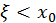и в силу возрастания 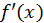имеем В этом случае получаем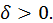

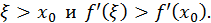Если теперь то Снова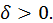

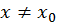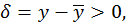Таким образом, при имеем т.е.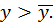

Отсюда вытекает, что при 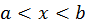кривая 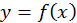расположена выше своих касательных и, значит, график функции 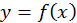будет вогнутым на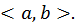

2) Аналогично доказывается, что есл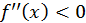и при 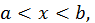то график функции будет выпуклым на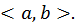

Здесь снова действует правило дождя .

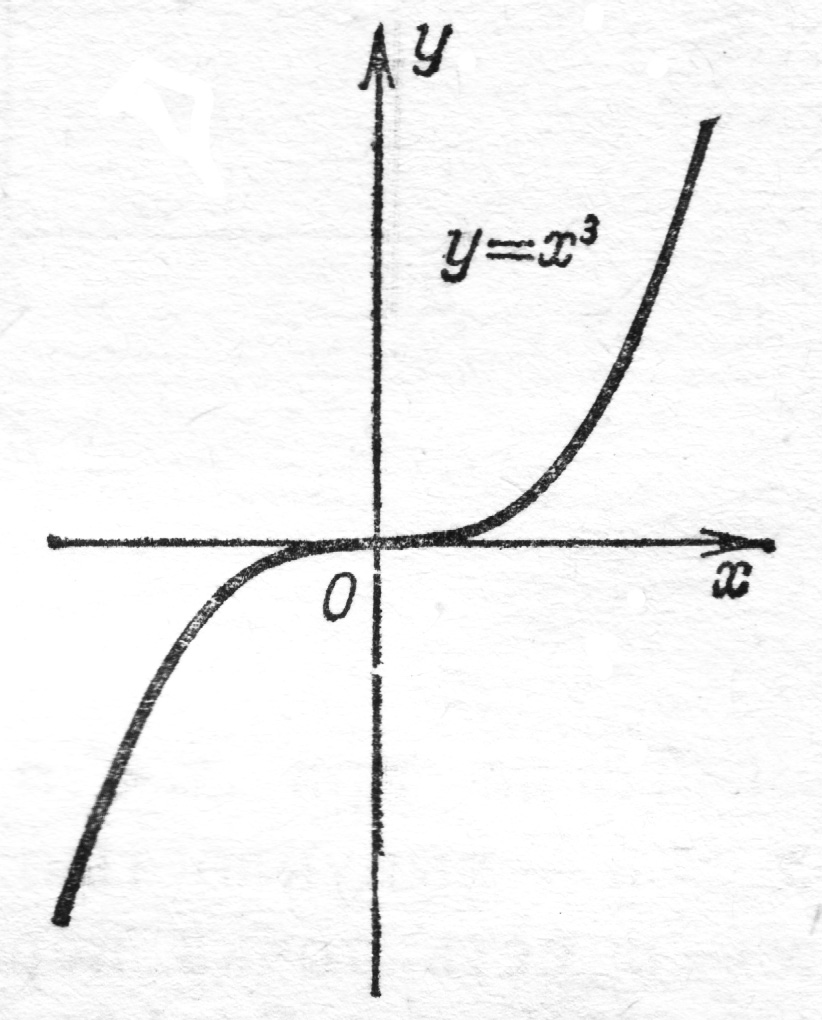
Пример. 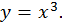Установить интервалы выпуклости и вогнутости.

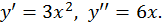
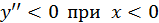, следовательно, при 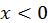кривая выпукла, а при 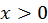- вогнута.

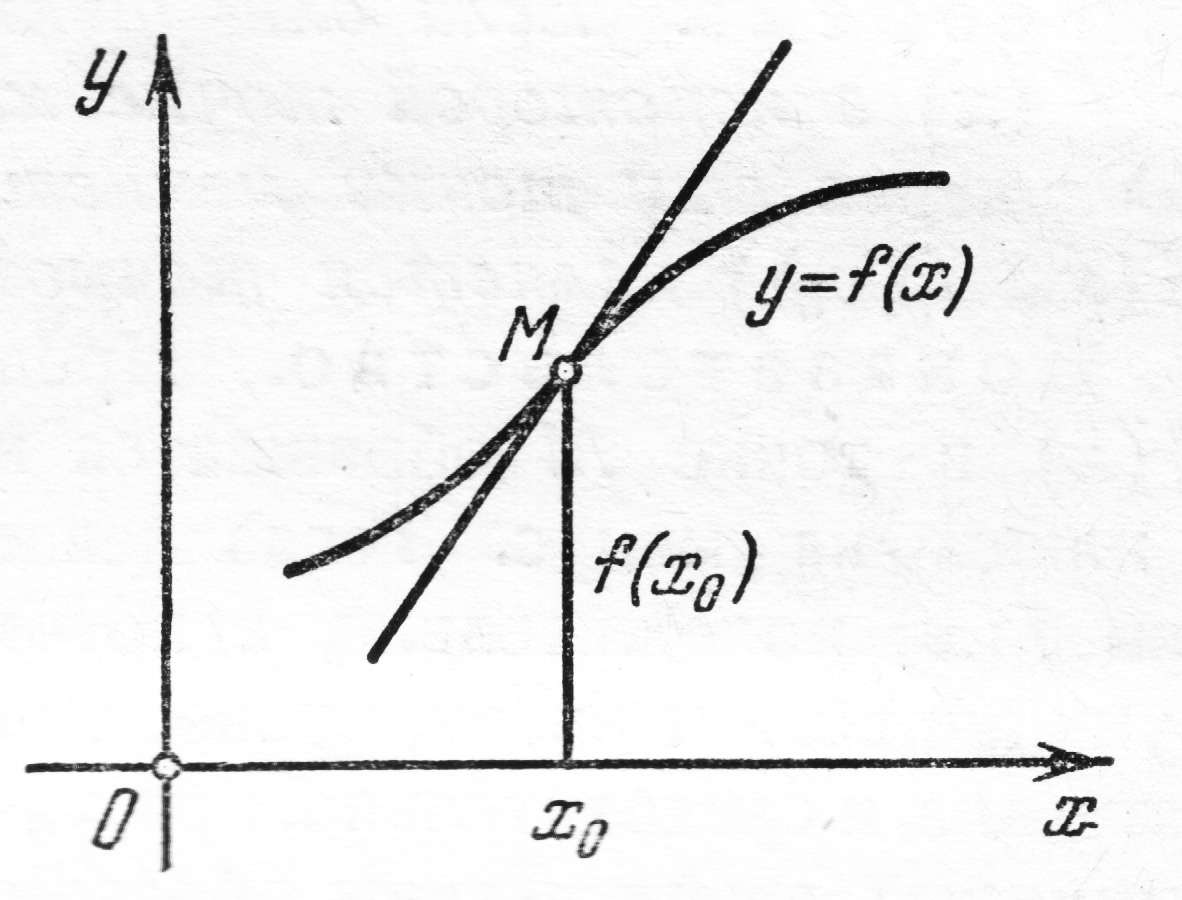Точки перегиба

Точкой перегиба графика дифференцируемой функции называется его точка, при переходе через которую кривая меняет свою вогнутость на выпуклость или наоборот.

Поиск по сайту: