Случай комплексных корней знаменателя

Напомним, что комплексные корни многочлена с действительными коэффициентами всегда попарно сопряжены. В разложении многочлена на действительные множители каждой паре комплексных корней многочлена соответствует выражение вида Если же комплексные корни имеют кратность то им соответствует выражение

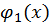Теорема 2. Если где многочлен не делится на то правильную рациональную дробь можно представить в виде суммы двух других правильных дробей следующим образом:

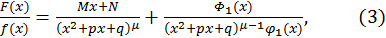
где многочлен, степень которого ниже степени многочлена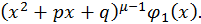

Доказательство. Напишем тождество:

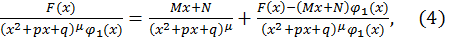
Справедливое при любых 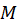и и определим и так, чтобы многочлен делился на Для этого необходимо и достаточно, чтобы уравнение имело те же корни что и многочлен Следовательно,

или

но есть определенное комплексное число, которое можно записать в виде 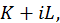где и некоторые действительные числа.

Таким образом,

отсюда

или

При этих значениях коэффициентов и многочлен

имеет корнем число а, следовательно, и сопряженное число Но в таком случае многочлен без остатка разделится на разности и а, следовательно, и на их произведение, т.е. на Обозначая частное от этого деления через получим:

Сокращая последнюю дробь в равенстве (4) на получим (3), причем ясно, что степень меньше степени знаменателя. Что и требовалось доказать.

Применяя теперь к правильной дроби результаты теорем 1 и2, мы можем выделить последовательно все простейшие дроби, соответствующие всем корням знаменателя 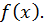Таким образом, из предыдущего вытекает следующий результат. Если

то дробь может быть представлена в виде:

(5)

Коэффициенты 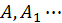можно определить из следующих соображений. Написанное равенство есть тождество, поэтому, приведя дроби к общему знаменателю, получим тождественные многочлены в числителях справа и слева. Приравнивая коэффициенты при одинаковых степенях получим систему уравнений для определения неизвестных коэффициентов 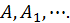Этот метод нахождения коэффициентов называется методом неопределенных коэффициентов. Наряду с этим для определения коэффициентов можно воспользоваться следующим замечанием: так как многочлены, получившиеся в числителях в правой и левой частях равенства после приведения к общему знаменателю, должны быть тождественно равны, то их значения равны при любых частных значениях 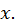Придавая частные значения, получим уравнения для определения коэффициентов. Этот метод нахождения коэффициентов называется методом произвольных значений.

Таким образом, мы видим, что всякая правильная рациональная дробь представляется в виде суммы простейших рациональных дробей. А интегрировать простейшие рациональные дроби мы умеем. Следовательно, мы теперь можем проинтегрировать любую дробную рациональную функцию.

Лекция 13.

Поиск по сайту: