Вероятность случайного события

3.1. Классическое определение вероятности события.

Вероятностью события называется числовая характеристика степени возможности появления события в испытании, которое можно повторять неограниченное число раз.

Если количество всех исходов испытания конечно и все исходы между собой равновозможны, то вероятность события А в этом испытании вычисляется по формуле

, (3.1)

где - число всех исходов испытания, - число благоприятных исходов, т.е. тех исходов, в которых появляется событие А.

Запишем эту формулу по-другому

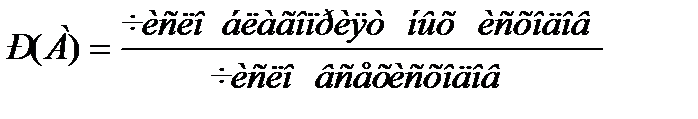(3.2)

Пример 3.1. Колода 36 карт. А - событие, состоящее в том, что наудачу вытащенная карта окажется бубновой мастью.

По условию, , , тогда

.

Основные свойства вероятности события:

1º. Пусть B - достоверное событие, т.е. , значит

.

2º. Пусть С - невозможное событие, т.е. 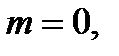значит

.

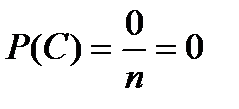3º. Пусть А - случайное событие, т.е. , значит

.

4º. .

Вывод:

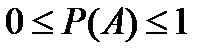
3.2. Геометрическое определение вероятности события.

Пусть область 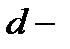часть области 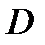, т.е. . Событие А - точка, наудачу брошенная в D, попадает и в d. Если вероятность попадания точки в d не зависит от ее места положения в D, то

.

Частные случаи:

1) Одномерный случай .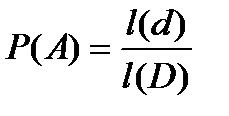

2) Двухмерный или плоский случай .

3) Трехмерный случай .

Поиск по сайту: