Случайные величины

8.1. Понятие случайной величины. Закон распределения дискретной случайной величины.

Одним из важнейших понятий теории вероятности является понятие случайной величины (в дальнейшем для краткости будем писать СВ)

Определение 17. Под СВ понимается переменная, которая в результате испытания принимает одно из своих возможных значений (какое именно – заранее неизвестно). Другими словами, СВ – это случайное событие, состоящее в появлении некоторого числа.

Примеры СВ: 1) число студентов на лекции;

2) количество бракованных деталей в данной партии;

3) дальность полета снаряда;

4) расход электроэнергии предприятием за месяц.

Определение 18. СВ называется дискретной (ДСВ), если множество ее значений конечное или бесконечное, но счетное.

Определение 19. Под непрерывной случайной величиной (НСВ) будем понимать величину, бесконечное несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) числовой оси.

Так, в приведенных выше примерах 1) и 2) имеем. ДСВ, а в примерах 3) и 4) – НСВ.

СВ будем обозначать прописными буквами латинского алфавита: X, Y, Z,… а их значения – соответствующими строчными буквами: x, y, z, …

Наиболее полным, исчерпывающим описанием СВ является ее закон распределения.

Определение 20. Законом распределения СВ называется всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.

Про СВ говорят, что она «распределена» по данному закону распределения или «подчинена» этому распределению.

Для ДСВ закон распределения может быть задан в виде таблицы, аналитически или графически.

Простейшей формой задания закона распределения ДСВ Х является таблица, в которой перечислены в порядке возрастания все возможные значения СВ и соответствующие им вероятности, т.е.

		…		…
		…		…

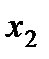
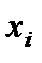
Такая таблица называется рядом распределения ДСВ.

Замечание 6. Так как события , , …, образуют полную группу, то . Эта единица как-то распределена между значениями СВ, отсюда и термин «распределение».

Для наглядности ряд распределения может быть изображен графически с помощью полигона (многоугольника) распределения вероятностей.

Определение 21. Полигон распределения вероятностей – это ломаная, соединяющая точки с координатами () (рис.1).

Рис.1

Пример 8.1. Вероятность того, что нужный товар есть в продаже, равна 0,3. В районе четыре магазина, где может быть этот товар. Составить закон распределения СВ Х – число магазинов, которые посетит покупатель в поисках товара.

Решение. Разберем эту задачу подробно. Возможные значения СВ Х находим, исходя из здравого смысла и представлении о ситуации. Очевидно, что здесь СВ Х может принимать значения 1, 2, 3 и 4. Теперь найдем вероятности, с которыми эти значения принимаются.

Х =1 – это означает, что покупатель приобрел товар в первом же магазине, который посетил, значит, .

В каком случае СВ Х примет значение 2?Если в первом магазине товар отсутствует с вероятностью 1-0,3=0,7, а во втором имеется. Таким образом, . Рассуждая аналогично, вероятность того, что СВ ,получим , т.е., в первых двух магазинах товара нет, в третьем удалось купить. При вычислении вероятности того, что с.в. Х=4 не забудем учесть следующий момент: такая ситуация возможна, если в трех посещенных магазинах товар отсутствует, в последнем есть, или нужного товара нет ни в одном магазине, Таким образом,

.

Теперь заполним таблицу:

	0,3	0,21	0,147	0,343

Контроль:

Пример 8.2. В лотерее разыгрывается автомобиль стоимостью 5000 у.е., 4 телевизора стоимостью 250 у.е., 5 телефонов стоимостью 200 у.е. Всего продается 1000 билетов по 7 у.е. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет.

Решение. Возможные значения СВ Х – чистого выигрыша на один билет, равны 0-7= -7 у.е. (если билет не выиграл), 200-7=193, 250-7=243, 5000-7=4993 у.е. (если на билет выпал выигрыш соответственно телефона, телевизора или автомобиля). Учитывая, что из 1000 билетов число невыигрышных составляет 990, а указанных выигрышей соответственно 5, 4, и 1, и, используя классическое определение вероятности, получим:

, ;

, .

Получим ряд распределения

	-7
	0,99	0,005	0,004	0,001

Контроль: .

8.2. Математические операции над случайными величинами.

Вначале введем понятие независимости СВ.

Определение 21. Две СВ называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина. В противном случае СВ называются зависимыми.

Определим математические операции над ДСВ.

Пусть даны две СВ:

Х:

		…		…
		…		…

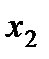
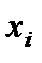
У:

		…		…
		…		…

Определение 21. Произведением СВ Х на постоянную величину называется СВ, которая принимает значения с теми же вероятностями

Определение 22. Степенью m СВ Х, т.е. , называется СВ, которая принимает значения с теми же вероятностями .

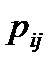Определение 22. Суммой (разностью или произведением) СВ Х и У называется случайная величина, которая принимает все возможные значения вида ( или ) с вероятностями , того, что СВ Х примет значение 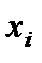, а СВ У – значение _:

.

Замечание 7. Если СВ Х и У независимы, то по теореме умножения вероятностей для независимых событий

Пример 8.3. Даны законы распределения двух независимых СВ:

Х:

	0,5	0,2	0,3

У:

	-2
	0,1	0,6	0,3

Найти законы распределения случайных величин:

1) ;

2) ;

3) ;

4) .

Решение. 1) Значения СВ будут: с теми же вероятностями. Получим закон распределения СВ :

:

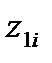
	0,5	0,2	0,3

2) Значения СВ. будут: с теми же вероятностями.

Получим закон распределения СВ :

:

	-8
	0,1	0,6	0,3

3) Для вычисления значений СВ найдем все возможные значения разностей: Зафиксируем и переберем все значения :

0-(-2)=2, 0-0=0, 0-2=-2.

Теперь проделаем то же самое для :

2-(-2)=4, 2-0=2, 2-2=0.

Аналогично для :

4-(-2)=6, 4-0=4, 4-2=2.

Составим вспомогательную таблицу, вероятности считаем в соответствие с замечанием 7:

:

			-2
	0,05	0,3	0,15	0,02	0,12	0,06	0,03	0,18	0,09

Эту таблицу необходимо улучшить. Так как среди девяти значений есть повторяющиеся, то заносим их в одну ячейку, а соответствующие вероятности складываем по теореме сложения вероятностей. Например, значение =2 может быть получено, когда , (с вероятностью 0,05); , (с вероятностью 0,12); и (с вероятностью 0,09). В результате получим распределение:

:

	-2
	0,15	0,36	0,26	0,2	0,03

Не забываем проверять сумму вероятностей:

контроль: .

4) Аналогично п. 3) считаем значения СВ , вспомогательную таблицу заполнять не будем. Помним, что значения СВ следует вносить в ряд распределения (в таблицу) в порядке возрастания.

При : ;

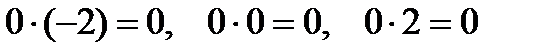при : ;

при : .

Составим закон распределения СВ :

	-8	-4
	0,03	0,02	0,8	0,06	0,09

Контроль: .

8.3. Числовые характеристики дискретной случайной величины.

Закон распределения ДСВ дает исчерпывающую информацию о ней, т.к. позволяет вычислить вероятности любых событий, связанных с СВ. Однако такой закон распределения бывает трудно обозримым, не всегда удобным (и даже необходимым) для анализа. Часто достаточно бывает знать некоторые количественные показатели, так называемые числовые характеристики.

Определение 23. Математическим ожиданием ДСВ Х называется сумма произведений всех ее значений на соответствующие им вероятности:

. (8.1)

Для краткости мы будем говорить «матожидание». Матожидание характеризует среднее значение СВ.

Пример 8.4. Вычислить для СВ из примера 8.2.

Решение.

,

т.е. средний выигрыш равен нулю. Полученный результат означает, что вся выручка от продажи билетов лотереи идет на выигрыши.

Рассмотрим свойства матожидания.

1º.

2º.

3º.

4º.

5º.

6º.

Только математическое ожидание не может в достаточной степени характеризовать СВ. Рассмотрим обычную житейскую ситуацию: средняя зарплата двух человек, получающих 10000р и 90000р равна 50000р. Точно такое же значение имеет средняя заработная плата людей, получающих, например, 45000р и 55000р. Средние значения этих величин (заработных плат) одинаковы, но величины эти сильно отличаются своим отклонением (разбросом, вариацией, рассеиванием) относительно среднего значения. Характеристикой такого отклонения служит дисперсия.

Определение 23. Дисперсией СВ Х называется математического ожидание квадрата ее отклонения от математического ожидания:

. (8.2)

Дисперсия 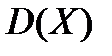имеет размерность квадрата случайной величины, т.е., если СВ Х измеряется в рублях или метрах, то 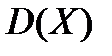измеряется в рублях в квадрате или метрах в квадрате, что не всегда удобно. Поэтому в качестве показателя рассеивания используется также величина .

Определение 24. Средним квадратическим отклонением СВ Х называется арифметическое значение корня квадратного из ее дисперсии:

. (8.3)

Отметим свойства дисперсии СВ:

1º. .

2º. .

3º.

4º. .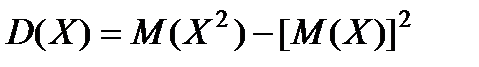

Замечание 8. Дисперсию удобнее вычислять по свойству 4, чем по формуле (8.2).

Пример 8.5. Дан закон распределения СВ Х.

	-2
	0,15	0,36	0,26	0,2	0,03

Найти числовые характеристики.

Решение.

;

Замечание 9. При вычислении дисперсии не забываем вычесть квадрат математического ожидания и следим, чтобы дисперсия была положительная. Если она получилась отрицательная, значит, ошиблись в вычислениях.

Числовые характеристики призваны в сжатой форме выражать наиболее существенные черты распределения СВ. Обращаем внимание на то, что сама величина Х – случайная, а ее числовые характеристики являются величинами неслучайными, постоянными.

В теории вероятности числовые характеристики играют большую роль. Часто удается решить вероятностные задачи, оперируя лишь числовыми характеристиками. Применение вероятностных методов для решения практических задач в значительной мере определяется умением пользоваться ими, оставляя в стороне законы распределения.

8.4. Функция распределения случайной величины.

Закон распределения не является универсальной возможностью описания СВ. Для этого возможен и другой подход: рассматривать не вероятности события для разных х (как это мы делаем в ряде распределения), а вероятности события , где х – текущая переменная.

Определение 25. Функцией распределения СВ Х называется функция , выражающая для каждого х вероятность того, что СВ Х примет значение, меньшее х:

. (8.4)

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка Х попадет левее заданной точки х.

Рассмотри общие свойства .

1º. .

Это свойство очевидно, т.к. - вероятность.

2º. есть неубывающая функция.

3º. .

Пример 8.6. Дан закон распределения СВ Х.

	0,4	0,1	0,3	0,2

Найти ее функцию распределения и построить график этой функции.

Решение. Искать функцию распределения будем следующим образом: т.к. случайная величина Х принимает 4 значения, которые делят числовую ось на 5 интервалов ((-∞; 1]; (1; 4]; (4;5]; (5;7]; (7;+∞)), то представляет собой составную функцию из пяти выражений. При = т.к. х не принимает значения меньше 1, при = . Если = . Далее рассуждая аналогично, получим

=

Изобразим функцию графически (рис. 2)

Рис.2.

Поиск по сайту: