АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Построение закона распределения случайной величины

Читайте также:
  1. B) Наличное бытие закона
  2. Акты реагирования прокурора на нарушения закона
  3. Алгоритм открытого распределения ключей Диффи - Хеллмана.
  4. Анализ распределения и использования чистой прибыли
  5. Анализ распределения чистой прибыли
  6. Аукционный порядок распределения земельных участков.
  7. Верховенство закона
  8. ВИДЫ ЭМПИРИЧЕСКИХ графикОВ распределения
  9. Возражает ли тантра против того, что человек следует некоторым законам жизни и считает их нравственными?
  10. Вопрос 1 Числовые характеристики статистического распределения
  11. Вопрос 2 Доверительный интервал для нормального распределения.
  12. Вопрос 2. Построение доверительного интервала при неизвестном законе генерального распределения.

Задание №1.

Случайная переменная Х определяется как сумма выпавших очков при бросании двух игральных костей. Найдите распределение вероятностей для случайной величины Х.

Методические указания по выполнению задания:

Если бросить две игральные кости, то возможны 36 исходов эксперимента, поскольку на первой кости может выпасть любое число от 1 до 6 и то же самое – на второй. Случайная переменная Х, определяемая как их сумма, может принимать одно из 11 числовых значений – от 2 до 12:

Игральная кость I Игральная кость II
           
             
             
             
             
             
             

Закон распределения данной случайной величины имеет следующий вид:

хi                      
рi 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36

Задание № 2.

Дан ряд распределения случайной величины Х:

хi      
рi 0,4 0,1 0,5

Найти функцию распределения.

Методические указания по выполнению задания:

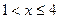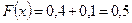В соответствии с определением при ; при ; при ; при . Итак:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 |

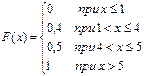
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)