 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема: Мультиколлинеарность. Фиктивные переменные. 1. Введение фиктивных переменных в уравнение множественной регрессии
Содержание занятия.
1. Введение фиктивных переменных в уравнение множественной регрессии.
2. Частная корреляция модели множественной регрессии.
Литература: [1] стр155-169, [3] стр200-216, стр262-282
Задание 1 Пусть по данным о 20 рабочих цеха оценивается регрессия заработной платы рабочего за месяц от количественного фактора – возраст рабочего (лет) и качественного фактора – пол.
| № | Заработная плата рабочего за месяц, $, у | Возраст рабочего, лет, х1 | Пол, м/ж, х2 |
| Ж М Ж Ж М М Ж М М М Ж М М М Ж М М М Ж М |
Построить модель множественной регрессии.
Методические указания по выполнению задания:
Введем в модель фиктивную переменную z, которая принимает два значения: 1 – если пол рабочего мужской; 0 – если пол женский. Построим модель вида:  .
.
Для оценки параметров модели используем метод наименьших квадратов. Построим систему нормальных уравнений: 
В результате решения системы получим оценки: 
Уравнение регрессии:  .
.
Интерпретация параметра с=10,32 при фиктивной переменной: у мужчин зарплата в среднем выше, чем у женщин при одном и том же возрасте мужчины и женщины на 10,32$.
Задание №2
Изучается зависимость выработки продукции на одного работника у (тыс. д.ед.) от ввода в действие новых основных фондов х1 (% стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%).
| Номер предприятия | у | х1 | х2 |
| 3,9 3,9 3,7 4,0 3,8 4,8 5,4 4,4 5,3 6,8 6,0 6,4 6,8 7,2 8,0 8,2 8,1 8,5 9,6 9,0 | |||
| средние | 9,6 | 6,19 | 22,3 |
Определить средние коэффициенты эластичности, частные коэффициентов корреляции.
Методические указания по выполнению задания:
Средние коэффициенты эластичности определяются по формуле: 
Для данного уравнения множественной регрессии (построенном на предыдущем занятии) получим:


С увеличением основных фондов на 1% выработка продукции на одного работника увеличивается на 0,609% при устранении влияния действия удельного веса рабочих высокой квалификации в общей численности рабочих. С увеличением удельного веса рабочих высокой квалификации в общей численности рабочих на 1% выработка продукции на одного работника увеличивается на 0,199% при устранении влияния основных фондов.
Линейные коэффициенты частной корреляции рассчитываются по рекуррентной формуле:
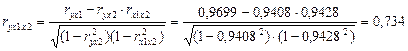
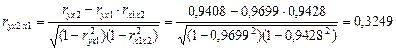
Сравнивая полученные результаты, видно, что более сильное воздействие на выработку продукции оказывает действие новых основных фондов.
Поиск по сайту: