 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема: Динамический ряд. 1. Расчет автокорреляции уровней временного ряда
Содержание занятия.
1. Расчет автокорреляции уровней временного ряда.
2. Расчет параметров трендов.
Литература: [1] стр234-239,[2] стр138-139
Задание №1 Имеются условные данные о средних расходах на конечное потребление (усл. д.ед.) за 8 лет:
| t | ||||||||
| yt |
Рассчитать коэффициент автокорреляции первого порядка.
Методические указания по выполнению задания:
Расходы на конечное потребление в текущем году зависят от расходов на конечное потребление предыдущих лет, поэтому определим коэффициент корреляции между рядами
yt и yt-1 и измерим тесноту связи между расходами на конечное потребление текущего и предыдущего годов. Формула для расчета коэффициента корреляции имеет вид: 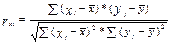
В качестве переменной х рассмотрим ряд y2, y3,…, y8; в качестве переменной y - ряд y1, y2,… y7. Тогда приведенная формула примет вид:
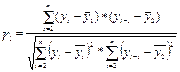 где
где 
Заполним таблицу:
| t | yt | yt-1 | 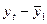
| 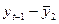
| 
| 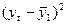
| 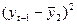
|
| - | - -3,29 -3,29 -1,29 -0,29 0,71 2,71 4,71 | - -3 -2 -2 | - 9,87 6,58 2,58 0,00 0,71 5,42 18,84 | - 10,8241 10,8241 1,6641 0,0841 0,5041 7,3441 22,1841 | - | ||
| итого | 53,4287 |
где 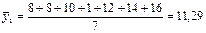
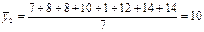 .
.
Используя формулу, получаем коэффициент автокорреляции первого порядка: 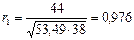
Полученное значение свидетельствует об очень тесной зависимости между расходами на конечное потребление текущего и непосредственно предшествующих годов и, следовательно, о наличии во временном ряде сильной линейной тенденции. Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков.
Задание №2. Имеются данные об урожайности овощей в хозяйствах области:
| Год | Урожайность овощей, ц/га |
| 49,2 41,7 46,0 67,3 69,0 73,6 85,8 92,4 98,4 94,4 |
1. Построить графики ряда динамики и трендов.
2. Рассчитать параметры уравнений трендов.
3. Выбрать наилучший вид тренда на основании графического изображения и значения коэффициента детерминации.
Методические указания по выполнению задания:
Построение графиков осуществляется с помощью Мастера диаграмм:
1) введите исходные данные;
2) активизируйте Мастер диаграмм: в главном меню выберите Вставка/Диаграмма
3) в окне Тип выберите График. Щелкните по кнопке Далее.
4) Заполните диапазон данных. Установите флажок размещения данных в столбцах (строках). Щелкните по кнопке Далее.
5) Заполните параметры диаграммы на разных закладках: названия диаграммы и осей; подписи данных и др. Укажите место размещения диаграммы на отдельном или на имеющемся листе. Щелкните по кнопке Готово.
Линия тренда может быть добавлена в построенный график. Для этого:
1) выделите область построения диаграммы; в главном меню выберите Диаграмма/Добавить линию тренда;
2) в появившемся диалоговом окне выберите вид линии тренда и задайте соответствующие параметры. Для полиномиального тренда необходимо задать степень аппроксимирующего полинома. В качестве дополнительной информации на диаграмме следует отобразить уравнение регрессии и значение коэффициента детерминации, установив соответствующие флажки на закладке Параметры. Щелкните по кнопке ОК.
Для вышеприведенных исходных данных получены следующие уравнения трендов и значения коэффициента детерминации 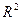 .
.
| Тип тренда | Уравнение | 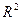
|
| Линейный | 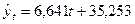
| 0,9206 |
| Полиномиальный второй степени | 
| 0,922 |
| Степенной | 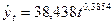
| 0,8034 |
| Экспоненциальный | 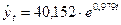 или или
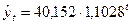
| 0,8846 |
| Логарифмический | 
| 0,8063 |
Исходные данные лучше всего описывает полином второй степени. Следовательно, в рассматриваемом примере для расчета прогнозных значений следует использовать полиномиальное уравнение.
Поиск по сайту: