Случайные события и их свойства

В основе теории вероятностей лежит понятие случайного эксперимента, т. е. эксперимента, который может закончиться любым из некоторого множества известных результатов, но заранее (до осуществления эксперимента) неизвестно каким.

Так, бросая игральную кость, нельзя быть заранее уверенным, что выпадает грань с номером 6.

В дальнейшем исходами будем называть различные результаты эксперимента.

Определение. Пространством элементарных исходов называется множество всех взаимно исключающих (т. е. не могущих наступить одновременно) исходов эксперимента.

Пространство элементарных исходов мы будем обозначать буквой

Определение. Событием называется любое подмножество Событие может состоять из одного или нескольких исходов, а может включать счетное или даже несчетное число исходов. События будут обозначаться прописными буквами А, В,... или же словами.

Будем говорить, что событие А наступило, если эксперимент заканчивается одним из исходов, входящих в событие А. Пример 1. Бросание игральной кости.

Здесь состоит из шести исходов, заключающихся в

выпадении грани с соответствующим номером. Событие А = {выпало четное число} состоит из трех исходов, т. е. А = {2, 4, 6}. Считаем, что А наступило, если при бросании игральной кости выпала грань с номером 2, 4 или 6.

Пример 2. Стрельба по мишени до первого попадания. Здесь где исход п = {попадание при первом

выстреле}, а исход н...нп, где «н встречается k» раз означает, что стрелок первые k раз промахнулся, а в (k + 1)-й раз мишень была поражена. В данном случае пространство элементарных счетным множеством.

Заметим, возвращаясь несколько назад, что выбор субъективен и диктуется условиями задачи, а, следовательно, может быть разным в одном и том же эксперименте.

Так, если в условиях примера 1 нас интересует лишь четное или нечетное число очков выпало, то логично в качестве где А = {2, 4, 6}, В = {1, 3, 5}.

Определение. называют событие, состоящее из всех исходов, принадлежащих либо А, либо В.

Определение. Произведением АВ двух событий А и В называют событие, состоящее только из тех исходов, которые входят в А и В одновременно.

Определение. Разностью А - В двух событий А и В называется событие, состоящее из исходов, входящих в А, но не входящих в В.

Если события изобразить множествами на плоскости, то результат определенных операций над событиями выглядит так, как представлено на рис. 7.1-7.3.

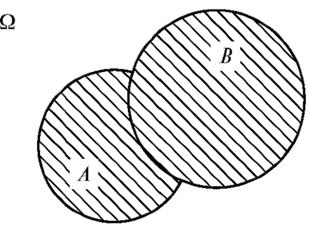
Рис. 1. Сумма событий А + В

Рис. 2. Разность событий А - В

Пример 3. Пусть при бросании игральной кости (см. пример 1) событие А = {1, 3, 5} = {выпало нечетное число очков}, а событие В = {3, 6} = {выпало число очков, кратное трем}. Тогда А + В = {1, 3, 5, 6}, АВ = {3}, А - В = {1, 5}, В - А = {6}.

Определение. Противоположным (дополнительным) для события А называется событие , состоящее из всех исходов, не входящих в А (рис. 7.4). Отметим, что

Рис. 3. Произведение событий АВ

Рис. 4. События A и

Пример 4. Противоположными событиям А и В из примера 2 являются события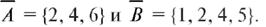

Определение. Событие называется достоверным (оно обязательно происходит). Событие называется невозможным.

Примером невозможного события при бросании игральной кости на ровную поверхность является событие, заключающееся в том, что игральная кость встала на вершину.

Определение. События А и В называются несовместными, если они не могут наступать одновременно.

Примером несовместных событий служат события А - В и В. Отметим, что если , то события А и В обязательно несовместны.

Определение. Говорят, что событие А содержится в событии ,

если все исходы события А входят в событие В. Так,

Приведем некоторые свойства операций над событиями:

Следует иметь в виду, что событие наступает, если происходит

«хотя бы одно» событие из а наступление события

означает, что ни одно событие из не произошло.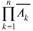

При бросании игральной кости а вероятности выпадения лю-

бой грани одинаковы и равны 1/6;

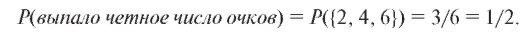
Пример 2. Какова вероятность угадать в лотерее 6 чисел из 49? Решение. Здесь равно совокупности всех сочетаний из 49 чисел по

. Благоприятствует выигрышу лишь одно событие. Поэтому

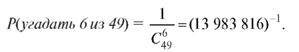
Пример 3. В клетке имеется 10 мышей: 3 белых и 7 серых. Наудачу вытаскивается одна мышь. Какова вероятность события А, что эта мышь белая.

Решение. В этом примере В соответствии с

формулой вероятность вытащить белую мышь равна 3/10.

Замечание. Слово «наудачу», употребленное в примере 3, является синонимом выражения «случайным образом» и означает выбор, при котором все комбинации элементов, которые могут быть выбраны, равновозможны.

Пример 4. Технический контроль из партии в 10 изделий проверяет взятые наудачу 3 изделия. Партия не принимается, если среди трех проверяемых изделий окажется хотя бы одно бракованное. Определить вероятность приемки партии, если в ней окажется 5 бракованных изделий.

Решение. Обозначим через А событие, состоящее в том, что партия изделий будет принята. Общее число исходов, состоящее в проверке

трех наудачу взятых изделий из 10, равно 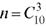, т. е. числу сочетаний

из 10 по 3. Событию А благоприятствуют исходов. Таким обра-

зом, получаем

Пример 5. При наборе телефонного номера абонент забыл две последние цифры и наудачу набрал их, помня только, что эти цифры нечетные и различные. Найти вероятность того, что номер набран правильно.

Решение. В этой задаче порядок набора цифр важен. Поэтому для определения числа всех возможных исходов следует использовать теорему 7.3 о числе размещений. Количество благоприятных исходов здесь равно 1, так как правильным является только один номер. Следовательно, искомая вероятность равна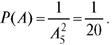

Пример 6. Пусть в группе из 10 человек четверо мужчин. Если случайным образом выбирают двух человек, то какова вероятность, что это: а) оба мужчины; б) обе женщины; в) один мужчина и одна женщина?

Решение. Обозначим события:

• А - выбирают двух мужчин;

• В - выбирают двух женщин;

• С - выбирают одного мужчину и одну женщину. Число всех исходов

Число выбора двух мужчин из четырех и двух женщин из шести: По формуле (7.3) имеем

Наконец, существует 4 способа выбора одного мужчины и 6 способов выбора одной женщины. По теореме 7.1 о числе комбинаций количество способов выбора двух человек обоего пола равно 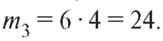Таким образом,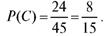

Пример 7. Из 20 человек, одновременно заболевших гриппом, 15 выздоровели полностью за 3 дня. Предположим, что из этих 20 человек случайным образом выбирают 5. Какова вероятность того, что за 3 дня из этих человек выздоравливают: а) 5 человек; б) 4 человека; в) никто не выздоравливает?

Решение. Определим события:

• А - за 3 дня выздоравливают 5 человек;

• В - за 3 дня выздоравливают 4 человека;

• С - за 3 дня не выздоравливает никто.

Число всех исходов равно .

Число способов выбора из 15 выздоровевших пяти человек -

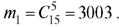Таким образом, .

Число способов выбора из 15 выздоровевших четырех человек - , одного невыздоровевшего из пяти 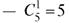. По теореме 7.1

число способов выбора 5 человек, из которых выздоравливают за 3 дня только четверо, равно Следовательно

Число способов выбора пяти невыздоровевших из пяти человек равно 1, откуда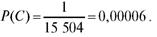

Пример 8. На полке 6 книг по математике и 4 по физике. Найти вероятность того, что среди выбранных наудачу пяти книг будут три по математике и две по физике.

Решение. Три книги по математике можно выбрать способами, а две книги по физике способами.

Пять книг, среди которых три по математике и две по физике, по теореме о числе комбинаций можно выбрать способами.

Число всех исходов равно . Искомая вероятность по

формуле (7.3) равна .

Пример 9. В клетке 6 белых и 4 серых мыши. Случайным образом извлекают 3 мыши. Вычислить вероятность для 4 возможных комбинаций цвета мышей.

Решение. Обозначим:

• б - белая мышь;

• с - серая мышь;

• - события, состоящие в появлении одной из возможных комбинаций цвета мышей

Число всех исходов равно(всего мышей 10, выбираем

3).

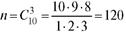
Число способов выбора из шести белых мышей трех равно 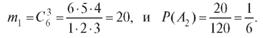Число способов выбора из четырех серых мышей трех равно

Событие A₃ состоит в том, что из шести белых мышей нужно выбрать одну - это способов, и из четырех серых мышей выбрать две -

это способов. Общее количество вариантов будет равно

Рассуждая аналогично, найдем общее число способов выбора двух белых и одной серой мыши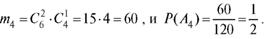

Пример 10. В коробке 5 одинаковых изделий, причем 3 из них окрашены. Наудачу извлечены 2 изделия. Найти вероятность того, что среди отобранных изделий: а) одно окрашено; б) два окрашены; в) хотя бы одно окрашено.

Решение. Обозначим события:

• А - окрашено одно изделие из двух извлеченных;

• В - окрашены два;

• С - оба не окрашены.

Число всех исходов определяется как

Так как окрашено одно изделие, то второе не окрашено и, следовательно,

Поскольку из двух извлеченных изделий окрашены два, то неокрашенных нет вовсе и

Здесь

Пример 11. Из пяти карточек с буквами А, Б, В, Г, Д наугад выбираются три и располагаются в ряд в порядке появления. Какова вероятность того, что получится слово «два»?

Решение. Так как положение буквы в комбинации имеет значение, то для определения общего числа возможных исходов следует пользоваться размещениями: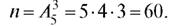

Здесь m = 1, так как требуется получить только одно слово «два». Следовательно, .

Свойства вероятностей:

Свойство 1. в силу условия нормировки (1).

Свойство 2. , так как в (2) сумма не содержит слагаемых.

Свойство 3. Если (в сумме (2), определяющей

Р(В), присутствуют дополнительные по сравнению с Р(А) неотрицательные слагаемые). Свойство 4. что следует из свойств 3 и 1.

Свойство 5. так как по свойству 1

Свойство 5 важно в практическом отношении, так как позволяет вычислить вероятность события А, если известна вероятность противоположного события A.

Пример 1. Из полного набора костей домино наугад берутся пять костей. Найти вероятность того, что среди них будет хотя бы одна с шестеркой.

Решение. При решении этой задачи удобно использовать свойство 5 вероятностей, перейдя к противоположному событию «среди пяти отобранных костей домино нет ни одной шестерки».

Число всех исходов

Поскольку количество костей домино, не содержащих шестерку, равно 21, то число исходов, благоприятствующих противоположному событию, будет:

Отсюда (см. (3))

Из свойства 5 вероятностей и свойства 15 операций над событиями вытекает следующее соотношение: для любого набора событий ,

2,..., n,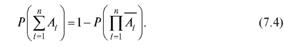

Равенство (7.4) означает, что вероятность того, что произошло «хотя бы одно» событие из 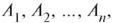можно найти, вычитая из 1 вероят-

ность того, что не произошло ни одно событие из В некото-

рых случаях таким приемом удобно пользоваться.

Свойство 6. Для любых событий А и В имеет место формула сложения вероятностей

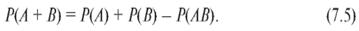
При проверке равенства (7.5) полезно воспользоваться геометрической иллюстрацией событий А + В и АВ (см. рис. 1 и 2), интерпретируя вероятности событий как площади соответствующих им изображений.

Пример 2. В марте 7 дней шел снег, 10 дней - дождь, из них 4 дня - снег с дождем. Найти вероятность того, что в выбранный наугад день шел дождь или снег.

Решение. Пусть А = { шел снег} и В = { шел дождь}. По формуле (7.5)

Р(шел дождь или снег) =

Пример 3. Из 100 студентов, находящихся в аудитории, 50 человек знают английский язык, 40 - французский, 35 - немецкий. Английский и французский знают 20 человек, английский и немецкий - 8, французский и немецкий - 10. Все три языка знают 5 человек. Один из студентов вышел. Определить вероятности следующих событий:

1. Вышедший студент знает английский и французский языки. Решение. Введем события:

• А - знает английский;

• В - знает французский. Тогда

2. Знает английский или немецкий языки. Решение. Событие: С - знает немецкий. Тогда

3. Знает немецкий или французский языки. Решение.

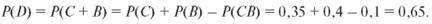
4. Кроме английского языка, знает или французский, или немецкий. Решение.

Из формулы сложения вероятностей можно вывести несколько следствий.

Следствие 1. Если события А и В несовместны, то

)

Пример 4. Определить вероятность того, что партия из 15 изделий, среди которых 5 бракованных, будет принята после выборочного контроля 4 вместе взятых изделий. Условием приемки является обнаружение не более одного бракованного среди 4 проверяемых изделий.

Решение. Введем обозначения:

• А - событие, состоящее в том, что партия изделий принята;

• В - все четыре проверяемые изделия качественные;

• С - среди четырех проверяемых одно изделие бракованное. Очевидно, что А = В + С (причем события В и С несовместны),

Следствие 2. Если события попарно несовместны, т. е.

для любых то

Пример 5. В клетке находится 10 мышей, причем 4 из них серые. Наугад берут трех мышей. Найти вероятность того, что хотя бы одна мышь серая.

Решение. Определим события:

• А - одна мышь серая, две - нет;

• В - две серые, одна - нет;

• С - все серые;

• D - ни одной серой;

• Е - хотя бы одна мышь серая.

События А, В и С являются несовместными, поэтому

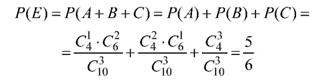
или (с учетом того, что

Поиск по сайту: