Математическое ожидание и дисперсия

Пусть мы измеряем случайную величину N раз, например, десять раз измеряем скорость ветра и хотим найти среднее значение. Как связано среднее значение с функцией распределения?

Будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших N оно стремится ко вполне конкретному числу – математическому ожиданию M_x. В данном случае M_x = 3,5.

Каким образом получилась эта величина? Пусть в N испытаниях раз выпало 1 очко, раз – 2 очка и так далее. Тогда 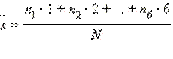При N → ∞ количество исходов, в которых выпало одно очко, Аналогично, Отсюда

. Элементы комбинаторики

Комбинаторика - это раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных элементов.

Теорема 7.1 (о числе комбинаций). Пусть имеется m множеств по

элементов в каждом. Выбрать по одному объекту из каждого множества можно способами.

Пример 1. Из трех классов спортивной школы надо составить команду по одному ученику от класса. Сколько различных команд можно составить, если в классах 18, 20 и 22 ученика соответственно.

Решение. Ответ на вопрос этого примера вытекает из теоремы 7.1 при m = 3, n₁ = 18, n₂ = 20, n₃ = 22. Всего можно составить 18 • 20 • 22 = 7920 команд.

Определение. Множество из n элементов называется упорядоченным, если каждому его элементу поставлен в соответствие свой номер от 1 до n.

Если 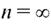, то множество называется счетньм. Определение. Упорядоченные наборы, составленные из всех элементов данного конечного множества, называются перестановками этого множества.

Пример 2. Множество из трех элементов {1, 2, 3} имеет следующие перестановки (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Всего их шесть.

Теорема 7.2 (о числе перестановок). Число всех перестановок множества из n элементов определяется формулой (считаем, что по определению

Пример 3. Цифры 0, 1, 2, 3 записаны на 4-х карточках. Сколько различных 4-значных цифр можно составить из этих карточек?

Решение. Число различных комбинаций из 4-х цифр равно 4!; 3! комбинаций, начинающихся с 0, следует исключить. В результате количество различных 4-значных чисел равно 4! - 3! = 18.

Определение. Упорядоченные наборы, состоящие из k элементов, взятых из данных n элементов, называются размещениями из n элементов по k.

Размещения отличаются друг от друга либо элементами, либо порядком.

Теорема 7.3 (о числе размещений). Число всех размещений из n элементов по k определяется формулой

Например, из множества {1, 2, 3} по два элемента можно (с учетом порядка) выбрать 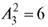способами: (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),

(3, 2).

При k = n из теоремы 7.3 следует теорема 7.2, т. е.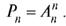

Пример 4. Сколько имеется вариантов занятия трех призовых мест 8-ю спортсменами одного уровня?

Решение. Ответ дается формулой .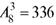

Определение. Неупорядоченные наборы, состоящие из k элементов, взятых из данных n элементов, называются сочетаниями из n элементов по k.

Сочетания отличаются друг от друга лишь элементами.

Так, для множества {1, 2, 3} сочетаниями по два элемента являются комбинации (1, 2), (1, 3), (2, 3).

Теорема 7.4 (о числе сочетаний). Число всех сочетаний из n элементов по k определяется формулой

Коэффициенты называют биномиальными коэффициентами, так как они входят в формулу бинома Ньютона:

Пример 5. В турнире участвует 6 команд. Каждая команда должна сыграть с каждой одну игру. Сколько игр сыграно в турнире?

Решение. Различные пары команд образуют сочетания из 6 по 2, поскольку порядок среди двух команд, играющих в одной игре, нам безразличен. Следовательно, число игр будет равно

Пример 6. Сколькими способами можно выбрать 2 ампулы из упаковки, содержащей 10 ампул.

Решение. По аналогии с предыдущим примером

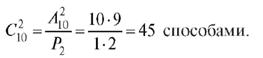
Пример 7. У 6 мальчиков и 11 девочек имеются признаки инфекционного заболевания. Чтобы проверить наличие заболевания, требуется взять выборочный анализ крови у 2 мальчиков и 2 девочек. Сколькими способами можно это сделать?

Решение. Количество способов выбора двух мальчиков:

Количество способов выбора двух девочек:

Поскольку каждая пара мальчиков может быть взята с каждой парой девочек, то по теореме 7.1 имеем:

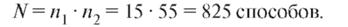
Поиск по сайту: