Раздел 2. Теория вероятностей и математическая статистика

Практическая работа № 7 « Решение задачна применение операции дизьюнкции, коньюнкции, отрицание с множеством высказываний »:

Практическая работа № 8 «Нахождение чисел комбинаторики, вероятности события, математического ожидания, дисперсии случайной величины»

Практическая работа № 9 «Расчет выборочных характеристик: математического ожидания, дисперсии. Применение статистических методов. Этапы статистического исследования. Относительные величины, методика изображения. Практическое применение статистических показателей»

Практическая работа № 10 «Составление и решение практических задач»

Учебная цель: находить числа комбинаторики, дисперсию случайной величины, применять статистические методы.

Учебные задачи: научиться расчету выборочных характеристик, применять в практике статистические показатели.

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

· решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления.

знать:

· основные понятия и методы математического анализа;

· алгоритмы применения определенного интеграла;

· основные понятия и методы интегрального исчисления

Задачи практической работы:

1. Повторить теоретический материал по теме практической работы.

2. Ответить на вопросы для закрепления теоретического материала.

3. Решить вариант.

4. Оформить отчёт

Обеспеченность занятия (средства обучения):

1. Тетрадь для практических работ (обычная, в клетку).

2. Карточки-задания (25 штук).

3. Калькулятор (простой).

4. Ручка.

Краткие теоретические и учебно-методические материалы по теме практической работы:

Отрицанием высказывания х называется новое высказывание , которое является истинным, если высказывание х ложно, и ложным, если высказывание х истинно.
Отрицание высказывания х обозначается и читается «не х» или «неверно, что х».
Логические значения высказывания можно описать с помощью таблицы.

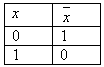
Таблицы такого вида принято называть таблицами истинности.
Пусть х высказывание. Так как также является высказыванием, то можно образовать отрицание высказывания , то есть высказывание , которое называется двойным отрицанием высказывания х. Ясно, что логические значения высказываний х и совпадают.
Например, для высказывания «Путин президент России» отрицанием будет высказывание «Путин не президент России», а двойным отрицанием будет высказывание «Неверно, что Путин не президент России».

Конъюнкцией (логическим умножением) двух высказываний х и у называется новое высказывание, которое считается истинным, если оба высказывания х и у истинны, и ложным, если хотя бы одно из них ложно.
Конъюнкция высказываний х и у обозначается символом х&у (, ху), читается «х и у». Высказывания х и у называются членами конъюнкции.
Логические значения конъюнкции описываются следующей таблицей истинности:

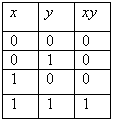
Например, для высказываний «6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится на 2 и 6 делится на 3», которое, очевидно, истинно.
Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний.

Дизъюнкцией (логическим сложением) двух высказываний х и у называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний х, у истинно, и ложным, если они оба ложны. Дизъюнкция высказываний х, у обозначается символом «x V у», читается «х или у». Высказывания х, у называются членами дизъюнкции.
Логические значения дизъюнкции описываются следующей таблицей истинности:

В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре логики союз «или» всегда употребляется в не исключающем смысле.

Импликацией двух высказываний х и у называется новое высказывание, которое считается ложным, если х истинно, а у - ложно, и истинным во всех остальных случаях.
Импликация высказываний х, у обозначается символом 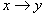, читается «если х, то у» или «из х следует у». Высказывание х называют условием или посылкой, высказывание у - следствием или заключением, высказывание 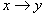следованием или импликацией.
Логические значения операции импликации описываются следующей таблицей истинности:

Употребление слов «если.... то...» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание х ложно, то высказывание «Если х, то у» вообще не имеет смысла. Кроме того, строя предложение вида «если х, то у» в обыденной речи, мы всегда подразумеваем, что предложение у вытекает из предложения х. Употребление слов «если..., то...» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается.
Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «Если х, то у». Если при этом известно, что х истинно и доказана истинность импликации 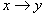, то мы вправе сделать вывод об истинности заключения у.

Эквивалентностью двух высказываний х и у называется новое высказывание, которое считается истинным, когда оба высказывания х, у либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквивалентность высказываний х, у обозначается символом , читается «для того, чтобы х, необходимо и достаточно, чтобы у» или «х тогда и только тогда, когда у». Высказывания х, у называются членами эквивалентности.
Логические значения операции эквивалентности описываются следующей таблицей истинности:

Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух членов эквивалентности и доказав истинность самой эквивалентности, мы зак­лючаем об истинности или ложности второго члена эквивалентности.

Поиск по сайту: