Функция распределения и плотность вероятности непрерывной случайной величины

Пусть Х является случайной величиной непрерывного типа. Множество значений такой случайной величины несчетно, поэтому мы не можем выписать в последовательность и занумерованность все ее значения и, следовательно, не можем задать ее закон распределения в виде таблицы. В этом случае на помощь приходит функция распределения, с помощью которой можно характеризовать закон распределения случайной величины любого типа. Случайная величина Х (любого типа) считается заданной, если известна ее функция распределения, т. е. функция

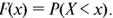
Рассмотрим некоторые основные свойства функции распределения F(x) произвольной случайной величины Х.

Прежде всего, как всякая вероятность, F(x) удовлетворяет при любом х неравенству 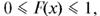так что график функции y = F(x) всегда лежит в полосе между прямыми y = 0, y = 1.

При помощи функции распределения F(x) можно всегда определить вероятность попадания случайной величины Х на промежуток [а; р) при любых значениях а и р.

В самом деле, если через А обозначить событие, состоящее в том, что через В - событие, со-

стоящее в том, что 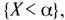и, нако-

нец, через С - событие то очевидно, что А = В + С.

Следовательно, по правилу сложения вероятностей для несовместимых событий откуда 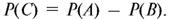Но

Поэтому окончательно

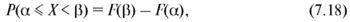
т. е. вероятность попадания случайной величины в промежуток равна приращению функции распределения на этом промежутке.

Так как вероятность неотрицательна, как всякая вероят-

ность, то из последнего равенства следует, что если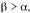

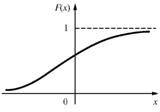
Рис. 7.7. Функция распределения непрерывной случайной величины

т. е. функция распределения любой случайной величины является неубывающей функцией.

Если случайная величина Х является ограниченной, т. е. все ее возможные значения лежат в каком-либо конечном отрезке 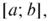мы будем иметь равенства

В общем случае, когда величина Х может быть и неограниченной, будут иметь место следующие соотношения:

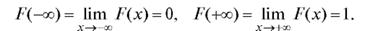
Примером может служить функция распределения случайной величины, распределенной по показательному закону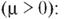

(7.19)

Если случайная величина Х принадлежит к непрерывному типу, то для любого x имеем равенство

Напомним, что для дискретных случайных величин отлично

от нуля, если x совпадает с каким-либо частным значением этой случайной величины.

Таким образом, любая непрерывная случайная величина Х не может быть характеризована вероятностями своих значений, поскольку все эти вероятности равны нулю.

Чтобы преодолеть эту трудность, вводится понятие плотности вероятности.

Определение. Плотностью вероятности, или дифференциальным законом распределения вероятностей, случайной величины Х называется функция f (x), определяемая равенством

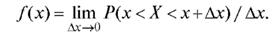
Рассмотрим свойства плотности вероятности.

Во-первых, очевидно, что поскольку вероятность неотрицательна.

Во-вторых, числитель правой части последней формулы может быть заменен разностью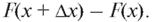

На основании определения производной получим выражение плотности вероятности через функцию распределения:

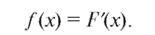(7.20)

Третье свойство плотности вероятности может быть получено, если сопоставить равенство (7.18) для непрерывной случайной величины с формулой Ньютона-Лейбница

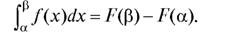(7.21)

Это сопоставление позволяет получить выражение для вероятности попадания случайной величины Х непрерывного типа в интервал через ее плотность вероятности f (x):

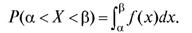(7.22)

Заменяя в последнем равенстве 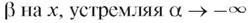и пользу-

ясь определением функции распределения, получим четвертое свойство плотности вероятности, позволяющее найти функцию распределения, если известна плотность вероятности:

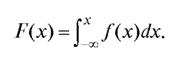(7.23)

Последнее, пятое свойство получим, если верхний предел х интеграла в последней формуле устремим к :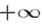

(7.24)

Это означает, что площадь, ограниченная осью абсцисс и графиком плотности вероятности, равна 1.

Отметим, что не всякая непрерывная случайная величина Х имеет плотность вероятности, но лишь та, функция распределения которой дифференцируема.

Пример 1. Дана функция распределения непрерывной случайной величины Х:

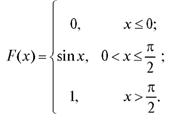
Рис. 7.8. Плотность распределения

Найти плотность вероятности f (x) и построить ее график. Решение.

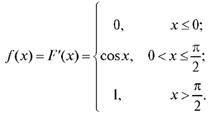
График плотности приведен на рис. 7.8.

Пример 2. Дана плотность распределения случайной величины Х:

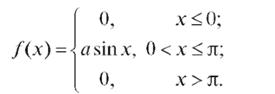
Определить коэффициент а и функцию распределения F(x). Решение.

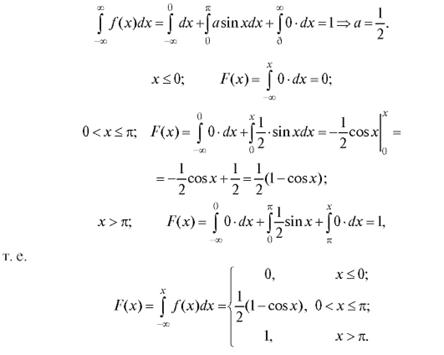
Поиск по сайту: