СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

До сих пор мы изучали способы вычисления вероятностей различных случайных событий. При этом под случайными событиями понималась любая качественная характеристика результата испытания. Однако существует много задач, решение которых требует изучения явлений, характер которых определяется не фактом появления или не появления того или иного случайного события, а зависит от некоторых величин, способных принять иные случайные значения. Такие величины в теории вероятностей называются случайными. Таким образом, если случайное событие есть качественная характеристика испытания, то случайная величина является количественной характеристикой испытания. Следует заметить, что понятие случайной величины является в известном смысле обобщением понятия случайного события, так как каждому случайному событию А можно всегда поставить в соответствие случайную величину, принимающую два значения, например 1 или 0, в зависимости от того, произошло событие А в результате данного испытания или не произошло.

Приведем примеры случайных величин:

• продолжительность жизни любого живого существа;

• число дефектных изделий в любой выборке данного объема;

• прибыль предприятия за любой фиксированный отрезок времени;

• погрешность любого измерения;

• время безотказной работы любого технического устройства;

• отклонения параметров данного устройства от номинальных значений.

Приведенные примеры с достаточной определенностью показывают, что со случайными величинами приходится иметь дело в самых разнообразных областях науки и техники.

Для полной характеристики случайной величины необходимо знать:

• множество ее возможных значений;

• как часто, т. е. с какой вероятностью, случайная величина принимает те или иные значения.

Такая характеристика случайной величины называется ее законом распределения. Закон распределения случайной величины может быть задан в различных формах в зависимости от типа случайной величины. Тип случайной величины определяется видом множества значений, которые может принимать рассматриваемая случайная величина. Особую

важность для технических приложений имеют два типа случайных величин: дискретного и непрерывного типа.

Определение. Случайная величина называется величиной дискретного типа или просто дискретной, если она может принимать конечное или счетное множество значений.

Определение. Случайная величина называется величиной непрерывного типа, если она может принимать любые значения в одном или нескольких заданных интервалах.

7.2.1. Закон распределения вероятностей дискретной случайной величины

Рассмотрим дискретную случайную величину X c конечным множеством значений

Определение. Совокупность всех значений случайной величины X и соответствующих этим значениям вероятностей называется законом распределения X.

Закон дискретной случайной величины может быть задан с помощью табл. 7.1.

Таблица 7.1

Очевидно, что всегда должно быть выполнено условие так как события образуют полную группу событий.

Важный пример дискретной случайной величины дает число m появлений некоторого события в серии последовательных испытаний, проведенных по схеме Бернулли.

Обозначим через X число появлений события А в n испытаниях, и пусть вероятность наступления события А в каждом испытании равна p.

Говорят, что случайная величина X имеет биномиальное распределение с параметрами n и p, если

Еще одним примером дискретной случайной величины является случайная величина X, имеющая распределение Пуассона с параметром

Напоминаем, что распределение Пуассона является предельным для биномиального распределения. Отметим также, что случайная величина X, имеющая распределение Пуассона, принимает бесконечное число значений.

Закон распределения дискретной случайной величины можно задавать по-другому, а именно с помощью так называемого интегрального закона распределения, или функции распределения вероятностей.

Определение. Функцией распределения F(x) случайной величины X называется вероятность того, что величина X примет значение, меньшее чем 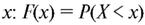, где x - произвольное вещественное число.

Заметим сразу же, что функция распределения вероятностей F(x) случайной величины Х является универсальной характеристикой Х, она существует для случайной величины любого типа.

Очевидно, что если Х - дискретная случайная величина, то ее функция распределения определяется посредством равенства

(7.17)

Пример 2. Построить ряд распределения случайной величины Х, представляющей собой число выпадения герба при двукратном бросании монеты.

Решение. Рассчитаем, а затем заполним табл. 7.3.

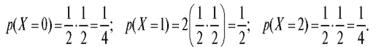
Таблица 7.3

Пример 3. Из партии в 25 изделий, среди которых имеются 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить ряд распределения случайного числа бракованных изделий, содержащихся в выборке.

Решение. Рассчитаем, а затем заполним табл. 7.4.

Таблица 7.4

Поиск по сайту: