Статистическое определение вероятностей

Классическое определение вероятностей, по существу, сводит понятие «вероятности» к понятию «равновозможности». Однако «равновозможность», представляя собой объективное свойство испытаний, определяемое условиями эксперимента, может быть установлена лишь с известной степенью точности.

Наше представление о симметричных игральных костях, монетах и т. п. было бы только иллюзией, не подтверждай правоту сделанных предположений данные опыта.

Многочисленные эксперименты открыли путь для статистического подхода к численному определению вероятностей, который особенно важен тогда, когда из теоретических соображений, подобных соображениям симметрии, значение вероятности заранее установить нельзя.

В соответствии с этим подходом вероятностью события А называется объективно существующая величина, около которой группируются относительные частоты наступления этого события при неограниченном увеличении числа испытаний.

Другими словами, , где n - общее число испытаний, а

m_A - число испытаний, в которых событие А наступило. Разумеется, условия, при которых проводится эксперимент, не должны изменяться от опыта к опыту.

Близость частоты и вероятности при многократном повторении одних и тех же экспериментов объясняется так называемым законом больших чисел.

Условные вероятности. Независимость событий

Рассмотрим вопрос о том, как определить вероятность какого-либо события А при условии, что уже произошло другое событие B.

Пусть, для примера, брошена игральная кость и нам неизвестен результат, однако известно, что выпало четное число очков. Мы же хотим, располагая этой информацией, найти вероятность того, что выпало число больше трех. Речь, следовательно, идет об условной вероятности события А = {выпало число больше трех} при условии, что произошло событие В = {выпало четное число} (обозначается ) - рис. 5.

Поскольку нам известно, что выпало либо 2, либо 4, либо 6 очков, и эти исходы равновозможны, а в такой ситуации событию А благоприятствуют лишь исходы 4 и 6, естественно считать, что

Формально это можно объяснить следующим образом: так как событие В произошло, мы в качестве нового пространства элементарных исходов берем все исходы, которые принадлежат В, а

Рис. 5. Иллюстрация к процедуре вычисления условной вероятности P(A/B)

благоприятствующими наступлению события А считаем исходы, входящие в А и В одновременно.

Таким образом, по формуле классической вероятности

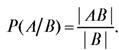
Принимая во внимание то, что последнее равенство можно переписать в виде 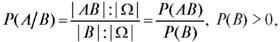приходим к следующему, согласующемуся с интуицией, определению.

Определение. Условная вероятность события А при условии, что произошло событие В с положительной вероятностью, задается формулой

В уже рассмотренном примерекак и

было сказано.

Из формулы (7.8) следует, что условная вероятность - это обычная вероятность, заданная на более узком пространстве элементарных исходов, поэтому для нее справедливы все свойства обычной вероятности.

В частности

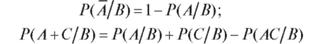
(формула сложения условных вероятностей).

Из равенства (7.8) вытекает формула умножения вероятностей:

(7.9)

Пример 1. В ящике m белых и n черных шаров. Какова вероятность вытащить подряд два белых шара?

Решение. Событие, вероятность которого требуется вычислить, можно представить в виде произведения событий АВ, где А = {первый шар белый}, В = {второй шар белый}. Вероятность события А вычисляется по

формуле (7.3) и равна 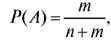условная вероятность

(если А произошло, то в ящике осталось (m - 1) белых

шаров, а всего - (m + n - 1) шаров). Остается воспользоваться формулой умножения вероятностей (7.9):

Тот же результат может быть получен с помощью формулы (7.3):

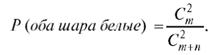
Формулу умножения вероятностей можно обобщить на случай n произвольных событий :

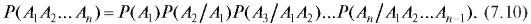
Определение. События А и В называются независимыми, если

Отсюда и из формулы умножения вероятностей следует, что

т. е. вероятность наступления события А не зависит от того, произошло В или нет (и наоборот). Так, если в ситуации примера 1, вытащив белый шар, вернуть его в ящик, то

Заметим, что из формулы сложения вероятностей (7.5) и из (7.11) следует, что если события А и В являются независимыми, то

Аналогично (7.11) определяется взаимная независимость событий 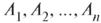в случае которой, в частности (см. также (7.4) и свойство 5),

С помощью формулы (7.13) очень просто сосчитать вероятность наступления хотя бы одного из n взаимно независимых событий.

Отметим, что понятие независимости отвечает всем интуитивным представлениям о независимости. В частности, если независимы события А и В, то независимы также события и т. д.

Пример 2. Некоторая вакцина эффективна на 75 % в формировании иммунитета. Вакцинировали двух человек. Пусть А и В - независимые события, состоящие в том, что соответственно первый и второй человек приобретают иммунитет. Найти вероятность того, что:

а) оба человека приобрели иммунитет;

б) первый приобрел иммунитет, а второй - нет;

в) оба не приобрели иммунитета. Решение.

7.1.7. Формула полной вероятности

Определение. Набор попарно несовместных событий 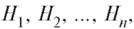сумма которых составляет достоверное событие, называется полной группой событий.

Теорема 7.5 (формула полной вероятности). Пусть события являются полной группой событий. Тогда для любого события А

(7.14)

Доказательство. В силу свойств операций над событиями (см.

п. 7.1.2)

Поскольку события попарно несовместны, то и события обладают тем же свойством. Поэтому в силу следствия 2 (см. (7.7))

Остается применить к слагаемым формулу умножения вероятностей.

Пример 1. Команда на хорошем поле выигрывает с вероятностью 2/3, а на плохом - с вероятностью 1/2. Известно, что 3/4 игр проводится на хорошем поле. Какова вероятность выиграть в выбранном наудачу матче?

Решение. Введем события А = {выигрыш}, = {плохое поле}, 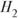= {хо рошее поле}. По условиям примера:

Пример 2. Вероятность брака при изготовлении детали равна 0,04. Приемка деталей производится по следующей системе контроля: годная деталь принимается с вероятностью 0,98, а бракованная - с вероятностью 0,1. Найти вероятность приемки детали.

Решение. Пусть событие А - деталь принята, - изготовлена хорошая деталь, - изготовлена бракованная деталь. Из условий найдем соответствующие вероятности:

А также:

• - вероятность того, что принятая деталь хорошая;

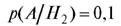• - вероятность того, что принятая деталь бракованная. Вероятность того, что деталь будет принята, на основании формулы(7.14) равна

Пример 3. Имеются три одинаковых ящика с шарами. В первом ящике 30 белых и 20 черных шаров, во втором - 15 белых и 15 черных шаров, в третьем - 5 белых и 15 черных шаров. Какова вероятность вытащить из случайно выбранного ящика черный шар?

Решение. Обозначим события:

• - выбран первый ящик;

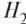• - выбран второй ящик;

• - выбран третий ящик.

Поскольку выбор того или иного ящика - события равновероятные, то

А также:

• - вероятность того, что черный шар вытащили из первого ящика;

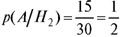• - вероятность того, что черный шар вытащили из второго ящика;

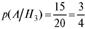• - вероятность того, что черный шар вытащили

из третьего ящика. По формуле (7.14) найдем искомую вероятность

Поиск по сайту: