Возникновение теории вероятностей. Вклад Маркова в её развитие

Теорию вероятностей нередко называют «наукой о случайном». На многих примерах можно убедиться в том, что массовые случайные явления тоже имеют свои закономерности, знание которых можно успешно использовать в практической деятельности человека.

Как наука теория вероятностей зародилась в XVII в. Возникновение понятия вероятности было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр. Слово «азарт», под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова hasard, буквально означающего «случай», «риск». Азартными называют те игры (карты, домино и т. п.), в которых выигрыш зависит главным образом не от умения игрока, а от случайности. Риск, играющий важную роль в этих играх, и приводит участников в необычайное состояние сильного увлечения и горячности.

Решение порой довольно сложных задач, с которыми обращались заинтересованные лица к Паскалю, Ферма, Гюйгенсу, способствовало разработке основных понятий и общих принципов теории вероятностей, в том числе и правил действия над ними. Отсюда не следует, конечно, заключать, что основоположники теории вероятностей рассматривали азартные игры как единственный или главный предмет разрабатывавшейся ими новой отрасли науки. На развитие теории вероятностей оказали влияние в первую очередь страховое дело, начатое в некоторых странах еще в XVI в. В XVI—XVII вв. учреждение страховых обществ и страхование судов от пожара распространилось во многих европейских странах. Азартные игры были для ученых только удобной моделью для решения задач и анализа понятий теории вероятности. Об этом заметил еще Гюйгенс в своей книге «О расчетах в азартной игре» (1657), которая была первой книгой в мире по теории вероятностей. Он писал: «...при внимательном изучении предмета читатель заметит, что он занимается не только игрой, а что здесь даются основы теории глубокой и весьма интересной». В труде Гюйгенса, как и в работах и письмах Паскаля и Ферма, содержится теорема сложения (или свойство аддитивности) вероятностей, которая утверждает, что вероятность наступления либо одного, либо другого из двух несовместимых (исключающих друг друга) событи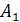й и 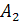равна сумме вероятностей.

Упомянутые ученые применяли также теорему умножения вероятностей, имеющую следующее содержание: вероятность совмещения двух независимых событий 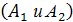равна произведению вероятностей каждого из них, т. е. 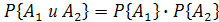. Гюйгенс первый ввел важное для теории вероятностей понятие "математического ожидания, которое получило дальнейшее развитие в трудах Даниила Бернулли, Даламбера и др. Математическим ожиданием игрока, имеющего вероятность Р для выигрыша суммы S, является произведение .

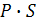Таким образом, в 60-е годы XVII в. были выработаны первые понятия и некоторые элементы теории вероятностей. В последующие два века ученые столкнулись с множеством новых задач, связанных с исследованием случайных явлений.

В начале XVIII в. Якоб Бернулли, развивая идеи Гюйгенса, разработал в своей книге «Искусство предложений», посмертно опубликованной в 1713 г., основы комбинаторики как аппарата для исчисления вероятностей, ввел ряд новых понятий и приемов и доказал одно из основных предложений теории вероятностей — «теорему Бернулли», являющуюся важным частным случаем так называемого «закона больших чисел», открытого в середине прошлого столетия П. Л. Чебышевым.

Благодаря теореме Бернулли теория вероятностей шагнула далеко за пределы вопросов азартных игр и применяется теперь во многих областях практической жизни и человеческой деятельности. Вот несколько примеров. В 1709 г. вышла в свет книга Нико­лая Бернулли «Примеры искусства предположений в приложении к юридическим вопросам». В своей книге «Теория случая» (2-е издание, 1738) Муавр применил теоретико-вероятностные принципы для вывода числа сочетаний и трактовки проблемы «пожизненных рент». При исследовании этой проблемы Муавр основывался на таблицах смертности населения, составленных с помощью исчисления вероятностей астрономом Э. Галлеем. Пользуясь работой Муавра, Т. Симпсон опубликовал в 1740 г. книгу «Природа и законы случая». В дальнейшем Симпсон, как и Котес, внес важный вклад в проблему оценки ошибок при различных наблюдениях. Шотландский математик Дж. Крег попытался применить учение о вероятностях даже к религии. В своем сочинении «Математические начала христианского богословия» (1699) он констатировал, что вера в истину христианской религии непрерывно ослабевает и, предположив, что она убывает пропорционально квадрату времени, вывел, что к 3150 г. религия совсем исчезнет.

Английский математик Т. Бейес явился автором теоремы (1763), носящей его имя. Любопытно отметить, что применением понятия вероятности к геометрии впервые занимался французский естествоиспытатель XVIII в. Ж. Бюффон, известный выдвинутым им положением о единстве растительного и животного мира.

Развитие естествознания и техники точных измерений, военного дела и связанной с ним теорией стрельбы, учения о молекулах в кинетической теории газов ставило перед учеными конца XVIII в XIX в. все новые и новые задачи из теории вероятностей. Одной из них была разработка теории ошибок измерений. Этой проблемой занимались многие математики, в том числе Котес, Симпсон, Лагранж, Лаплас. Последнему принадлежат обширные замечательные исследования, изложенные в его трудах: «Мемуар о вероятностях» (1778) и «Аналитическая теория вероятностей» (1814). Основы современной теории ошибок были созданы Лежандром и Гауссом. Важный вклад в теорию вероятностей внес С. Пуассон. Дальнейший расцвет теории вероятности связан с именем П. Л. Чебышева и его ближайших учеников А. А. Маркова и А. М. Ляпунова. В 25-летнем возрасте Чебышев написал первую свою работу в рассматриваемой нами области — «Опыт элементарного анализа теории вероятностей» (1845). Затем последовали другие его труды, в том числе работа «О средних величинах» (1867), в которой он чрезвычайно просто и элементарно доказал закон больших чисел в общей форме.

Большое практическое значение закона больших чисел состоит в том, что за математическое ожидание массовой случайной величины можно принять среднее арифметическое k ее значений, полученных опытным путем. Эта замена будет тем законнее, чем больше будет k число испытаний. Именно, основываясь на законе больших чисел, можно, например, судить о качестве большой партии пшеницы, содержащей десятки и сотни тонн, по нескольким сравнительно небольшим, скажем 200-граммовым, меркам, наполняемым случайно захваченными зернами из разных частей партии зерна. Такая выборка дает возможность установить с достаточной для практики степенью точности средний вес одного зерна и, значит, судить о качестве партии пшеницы в целом.

Работы П. Л. Чебышева, А. А. Маркова, А. М. Ляпунова и других русских математиков оказали большое влияние на дальнейшее развитие теории вероятностей. Возникшая во второй половине XIX в. в трудах Р. Клаузиуса, Дж. Максвелла, Л. Больцмана, Дж. Гиббса и других ученых, статистическая физика, в которой исследуются свойства систем с точки зрения их атомистического строения с помощью специальных статистических методов, как и другие отрасли науки и техники, поставила перед теорией вероятностей ряд совершенно новых проблем, в том числе и разработку общей теории массовых случайных процессов, изучающей случайные величины. Вот одна из типичных задач теории случайных процессов: исходя из показаний опыта о том, что распады атомов происходят в случайные моменты, определить, какова вероятность того, что за известный промежуток времени произойдет распад того или иного числа атомов. Это очень важно для изучения процесса радиоактивного распада.

Со второй половины XIX в. и поныне русские, а затем советские математики занимают ведущее место в развитии теории вероятностей. В первом десятилетии XX в. А. А. Марков положил начало теории последовательностей зависимых случайных величин, так называемых «цепей Маркова», которая вскоре стала важным средством изучения природы. Теорию цепей Маркова затем значительно развили С. Н. Бернштейн, В. И. Романовский, А. Н. Колмогоров и французские математики Ж. Адамар и И. Фреше. После того как трудами А. Н. Колмогорова, Е. Е. Слуцкого, А. Я. Хинчина и французского математика П. Леви была установлена связь между теорией вероятностей, с одной стороны, и теорией множеств и теорией функций действительного переменного — с другой, стало возможным добиться окончательного решения ряда классических проблем, поставленных еще в прошлом веке П. Л. Чебышевым.

А. Н. Колмогоров и А. Я. Хинчин положили начало общей теории случайных процессов, о которой говорилось выше. Разработка аксиоматики теории вероятностей означала новый этап в развитии этой науки. Первое по времени аксиоматическое построение теории вероятностей изложил в 1917 г. С. Н. Бернштейн. В настоящее время общепринятой стала аксиоматика, разработанная в 1933 г. А. Н. Колмогоровым. Среди видных современных советских математиков, разрабатывающих теорию вероятностей, следует назвать также Б. В. Гнеденко, внесшего важный вклад и в математическую статистику, Ю. В. Линника и многих других.

Поиск по сайту: