Создание теории групп и теории множеств 19-20 ст

Современная алгебра - чрезвычайно широкая и разветвленная область математики. Она объединяет большое число самостоятельных научных дисциплин. Их общим предметом являются алгебраические операции, представляющие собой далеко идущие абстракции операций элементарной алгебры.

Столь общие воззрения на природу и состав алгебры сложились по существу недавно, лишь в XX в. Вплоть до XIX в. основной задачей алгебры являлось решение алгебраических уравнений, понимаемое как нахождение корней уравнения с помощью рациональных, операций и операции извлечения корня. В поисках общей формулы математики перепробовали громадное количество методов и к самому концу XVIII в. были вынуждены фактически рассматривать поля и группы; еще не вводя этих понятий явно.

На рубеже XVIII и XIX вв. в алгебре были сделаны открытия необычайной важности. Они сопровождались введением в эту науку ряда новых понятий (в первую очередь понятия группы), которые легли в основу современной алгебры. Эти открытия повели к преобразованию всей алгебры в течение XIX в. Мы имеем в виду результаты К. Ф. Гаусса, Н. Г. Абеля и Э. Галуа, относящиеся к доказательству основной теоремы алгебры, доказательству неразрешимости в радикалах уравнений степени пять и созданию теории Галуа.

Галуа исследовал структуру нескольких конкретных классов разрешимых групп. Абель фактически исследовал структуру коммутативных групп. Он показал, что эти группы являются произведениями циклических групп. Однако понятие группы у него еще не было выделено.

Возникновение теории Галуа. Абель не смог дать общий критерий разрешимости уравнений с числовыми коэффициентами в радикалах. Но решение и этого вопроса не заставило себя долго ждать. Оно принадлежит Эваристу Галуа (1311-1832), французскому математику, скончавшемуся, как и Абель, в очень молодом возрасте. Его жизнь короткая, но наполненная активной политической борьбой, страстный интерес к математическим занятиям представляют яркий пример того, как в деятельности одаренного человека накопленные предпосылки науки претворяются в качественно новый этап ее развития. Галуа успел написать мало работ. В русском издании его работы, рукописи и черновые записи заняли лишь 120 страниц в книге маленького формата. Но значение этих работ огромно.

Эварист Галуа действительно открыл новые большие пути в математике, несмотря на то что его жизненный путь был чрезвычайно коротким: он умер в двадцатилетнем возрасте. Имя Галуа как одного из творцов современной математики тесно связано с понятием группы, с созданием теории групп и так называемой «теории Галуа».

Эта теория возникла из рассмотрения групп алгебраических преобразований при поисках решения в радикалах общих алгебраических уравнений степени выше 4-й. В известном смысле предшественниками Э. Галуа были Лагранж, П. Руффини и Н. Абель. Однако фундаментальные результаты в этой области получены были в 1830—1832 гг. именно Э. Галуа. Отсюда и название «теория Галуа». Галуа ввел по существу такие основные понятия, как «группа», «подгруппа», «нормальный делитель» и «поле». Он впервые ввел и термин «группа». Многие основные результаты своей теории Галуа получил еще в возрасте 16—18 лет и дважды представлял их в Парижскую Академию наук, однако даже крупнейшие французские математики того времени — Коши, Фурье, Пуассон — не сумели разобраться в работах Галуа и оценить их значение. Как республиканец и активнейший член общества «Друзей народа», Галуа публично выступал против королевского режима, за что подвергался гонениям и был дважды приговорен к тюремному заключению. По выходе из тюрьмы он был убит на дуэли, по-видимому, спровоцированной монархистами. Перед трагической смертью он написал письмо другу, в котором сжато изложил свои основные открытия. Работы Галуа были, однако, разобраны и опубликованы французским математиком Жозефом Лиувиллем лишь в 1846 г.

Широкое распространение и применение идей Э. Галуа началось только после опубликования объемистого труда известного французского математика Камилла Жордана — «Трактата о подстановках и алгебраических уравнениях» (1870), фактически явившегося, по словам самого автора, лишь пространным комментарием к трудам Галуа. Благодаря этой книге Жордана идеями теории групп увлеклись два молодых в то время одаренных математика — норвежец Софус Ли и немец Феликс Клейн. Первый применил идеи Галуа в теории дифференциальных уравнений (группы Ли), второй — в геометрии (Эрлангенская программа). Во второй половине 19 века теория групп развилась главным образом как теория групп преобразований. Со временем, однако, выяснилось, что и к другим объектам можно применить понятия и теоремы теории групп преобразований. Так возникла абстрактная, или общая, теория групп. В этой теории не рассматриваются объекты, над которыми производятся операции, ни существо этих операций, а исследуются лишь законы самих операций. Вот почему в настоящее время мы говорим, что произвольное множество G вместе с определенной на нем операцией “×” называется группой относительно этой операции, если выполняются следующие групповые аксиомы:

1) Произведение любых двух элементов какого-либо множества принадлежит тому же множеству.

2) Для любых трех элементов а,b, с из G имеет место ассоциативный закон, т. е.

3) В множестве G существует нейтральный элемент е, для которого при любом элементе 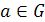. имеет место:

4) Для каждого элемента существует в обратный элемент , такой, что

.

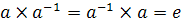Если для любых двух элементов а и b множества G имеет место 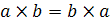, то группа называется коммутативной или абелевой, по имени молодого норвежского математика Абеля, открывшего значение таких групп для решения в радикалах алгебраических уравнений. Абстрактная теория групп позволяет рассматривать с единых позиций различные множества операций, тождественные с абстрактной точки зрения. Две группы, тождественные с абстрактной точки зрения, называются изоморфными, т. е. одного вида.

Так, например, группа перестановок двух электронов изоморфна, т. е. тождественна с абстрактной точки зрения группе осевых симметричных отражений плоскости.

В настоящее время идеи и методы теории групп применяются в различных областях естествознания, например в кристаллографии и в квантовой механике. Большой вклад в развитие теории Галуа, теории групп и ее приложений внесли Д. А. Граве, Н. Г. Чеботарев, О. Ю. Шмидт, Л. С. Понтрягин, А. Г. Курош, А. И. Мальцев и другие советские математики. Крупный русский кристаллограф, минералог и геометр академик Евграф Степанович Федоров (1853—1919) применил теорию групп к исследованию кристаллов.

Проблемы, связанные с понятиями бесконечности, дискретности и непрерывности, рассматривались в математике, как и в философии, древнегреческими мыслителями начиная с VI в. до н. э. Под влиянием сочинений Аристотеля эти проблемы широко обсуждались средневековыми учеными и философами в странах ислама и в Европе.

Множество — одно из первоначальных неопределяемых математических понятий. Мы встречались с разными числовыми множествами,, элементами которых являются числа той или иной природы (натуральные, целые, дробные, рациональные, иррациональные, действительные, комплексные, алгебраические, трансцендентные и др.). Можно говорить о множестве учащихся в классе, деревьев в лесу, корней данного уравнения, точек на данном отрезке и т. п. Желая подчеркнуть, что в понятии множества самое важное — это идея объединения элементов каким-либо общим признаком, Георг Кантор писал: многообразием или множеством я понимаю вообще всякое многое, которое можно мыслить как единое». Если множество имеет бесконечно много элементов, то оно называется бесконечным, например множество всех положительных чисел. Если же множество содержит конечное число элементов, то его называют конечным; таким является, например, множество сторон пятиугольника. Множество, не содержащее ни одного элемента, называется пустым.

Если отвлечься от природы и порядка элементов, то два конечных множества могут отличаться между собой только количеством своих элементов. Для сравнения таких двух множеств не обязательно пересчитывать их элементы. Достаточно поставить их элементы во взаимно однозначное соответствие. Если это можно полностью осуществить, то количество элементов в обоих множествах одинаково, в противном случае количество элементов одного из них (и понятно какого) больше другого.

Именно этот принцип установления взаимно однозначного соответствия между элементами двух множеств и положил Г. Кантор в начале 70-х годов прошлого века в основу сравнения и исследования бесконечных множеств. Если между элементами двух любых множеств можно установить взаимно однозначное соответствие, то говорят, что эти множества имеют одну и ту ж е мощность, или они равномощны, или эквивалентны. Равномощность обладает свойствами рефлексивности, симметрии и транзитивности. «В случае конечных множеств, — писал Кантор, — мощность совпадает с количеством элементов.». Вот почему мощность и называют также кардинальным (количественным) числом. Указанная простая и незначительная на первый взгляд идея Кантора привела его к замечательным открытиям, часто резко противоречащим обычной нашей интуиции. Так, в отличие от конечных множеств, на которые распространяется евклидова аксиома (целое больше частик бесконечные множества этому положению не подчиняются).

Множество называется бесконечным, если оно равномощно с одним из своих подмножеств. Конечным называют множество, не эквивалентное ни одному из своих подмножеств. Любое множество, эквивалентное множеству натуральных чисел, называют счетным, так как его элементы можно занумеровать: .

Еще более поразительным оказалось другое открытие, сделанное Кантором в 1873 г. Все три множества — натуральных чисел, рациональных чисел, алгебраических чисел — имеют одну и ту же мощность, иначе говоря, множество рациональных чисел и множество алгебраических чисел являются счетными множествами.

Cумма (или объединение) двух множеств, под которой понимают такое множество, которое содержит все такие и только такие элементы, которые содержатся хотя бы в одном из данных множеств. Сумма двух (и вообще конечного или счетного числа) счетных множеств есть счетное множество. Поэтому можно утверждать, что множество всех рациональных чисел счетно. Все вообще бесконечные множества счетны и, значит, равномощны и что поэтому и не имело смысла вводить понятие мощности. Однако в том же 1873 г. Кантор устанавливает существование неравномощных бесконечных множеств, доказав несчетность множества действительных чисел, значит, и множества точек прямой.

Кантор открыл, что не все бесконечные множества равномощны, что существуют разные степени бесконечности. На основе выше сказанного можно вывести то, что существуют иррациональные числа. Действительно, так как мощность действительных чисел больше мощности счетного множества рациональных чисел, то должны существовать и иррациональные числа. Аналогично рассуждая, мы приходим к выводу, что существуют неалгебраические, т. е. трансцендентные, числа и что их даже больше, чем алгебраических. Действительно, множество трансцендентных чисел несчетно, ибо если бы оно было счетным, подобно множеству алгебраических чисел, тогда должна была бы быть счетной и сумма их — множество действительных чисел, что неверно.

До Кантора считалось, что прямая содержит меньше точек, чем плоскость. Однако в 1878 г. Кантор доказал, что в единичном квадрате не больше точек, чем в единичном отрезке, указав способ установления взаимно однозначного соответствия между точками отрезка и квадрата.

Кантор ввел также трансфинитные порядковые числа. Дело в том, что конечные множества допускают лишь один тип упорядочения, характеризуемый порядковыми числами. Бесконечное же множество можно упорядочить различными способами. Для каждого возможного способа упорядочения или для всякого порядкового типа вводится его обозначение — трансфинитное число.

В отличие от большинства своих предшественников Кантор первый предпринял прямое и широкое исследование самой математической бесконечности, получив совершенно новые, неожиданные результаты. Некоторые из идей теории множеств были предвосхищены еще в 30-е и 40-е годы XIX в. Б. Больцано. Однако, как мы уже знаем, труды последнего были опубликованы слишком поздно, для того чтобы оказать какое-либо влияние на развитие математики. Кроме того, у Больцано не было понятия мощности множества, поэтому он был очень далек от того размаха, который получило учение о бесконечности в трудах Кантора. Для последнего, впрочем, исходным пунктом были его исследования вопроса о существовании трансцендентных чисел и вообще разработка учения о действительном числе, которой почти одновременно занимался и Р. Дедекинд. Развитию теории множеств способствовали также исследования в области учения о тригонометрических рядах Фурье и других математических дисциплин, возникших в первой половине XIX в.

В середине 80-х годов Кантор систематически изложил свое учение о множествах — абстрактную теорию множеств. К тому времени вышли также работа Г. Фреге «Основания арифметики» (1884), работа Р. Дедекинда «Что такое числа и чем они должны быть» (1887) и др., для которых, как и для работы Кантора, характерен новый, абстрактно-логический метод, широко использующий прямые логические рассуждения вместо вычислений и выкладок. Дедекинд, в частности, также получил важные результаты в области теории множеств.

Идеи и открытия Кантора встретили с самого начала их появления резкое сопротивление со стороны некоторых его современников, например со стороны члена Берлинской Академии наук немецкого математика Л. Кронекера. Последний был одним из приверженцев выдвижения на первый план дискретной величины, натуральных чисел, исходя из которых, было построено учение о рациональных и иррациональных числах. Тем не менее, уже в начале 90-х годов теория множеств получила почти всеобщее признание и стала широко применяться в математике. Однако в 1895 г. математики впервые столкнулись с одним парадоксом («антиномия Бурали-Форти»), за которым последовали другие парадоксы, или антиномии (от греческих слов «анти» — против и «номос» — закон), теории множеств. Одна из них, открытая английским философом и математиком Бертраном Расселом в 1902 г., относится к самым началам теории множеств и связана с понятием множества всех множеств. Каждое из обычных множеств, с которыми мы до сих пор встречались, не содержит само себя в качестве элемента; так, например, множество всех натуральных чисел само не является, конечно, натуральным числом. Такие множества назовем нормальными или обыкновенными. Однако существуют и такие необычные множества, которые являются собственными своими элементами, например множество всех вообще множеств. Такие множества назовем необыкновенными.

Теория множеств оказала огромное влияние на дальнейшее развитие нашей науки в XXв. и в настоящее время, теоретико-множественные методы проникли в очень многие области математики. Благодаря введению общего понятия множества стало возможным еще в последней четверти XIX в. дать строгое определение действительного числа, на котором зиждется понятие предела, и завершить, таким образом, обоснование анализа, начатое в. 20-х годах прошлого века. В связи с теорией множества возникали и развиваются новые математические дисциплины, например: теория функций действительного переменного, теоретико-множественная топология, функциональный анализ и др.

Поиск по сайту: