Создание комбинаторики

Комбинаторика занимается различного рода сочетаниями (соединениями), которые можно образовать из элементов некоторого конечного множества. Термин «комбинаторика» происходит от латинского слова соmbinа — сочетать, соединять.

Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые мы обозначаем через 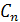, т. е. сочетания из п элементов, взятых по m, и знали формулу

В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановки. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стихов и поэтических произведений, например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы, состоящей из nслогов. В древней Индии, в Средней Азии и Китае была также известна частично таблица биномиальных коэффициентов. Однако как научная дисциплина комбинаторика сформировалась лишь в XVII в.

Независимо от Апиана (XVI в.), Штифеля и Тартальи французский математик Эригон (XVII в.) определяет в своей «Практической арифметике» (1634) . В книге «Теория и практика арифметики» (1656) другой французский автор, А. Такке, уже посвящает сочетаниям и перестановкам целую главу. Б. Паскаль в «Трактате об арифметическом треугольнике» и в «Трактате о числовых порядках» (1665) изложил учение о биномиальных коэффициентах, оперируя с ними как с сочетаниями. П. Ферма знал о связи магических квадратов и фигурных чисел с теорией соединений.

Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1666 г. работы «Рассуждение о комбинаторном искусстве», в котором впервые дано научное обоснование теории сочетаний и перестановок. Изучением «размещений» впервые занимался Якоб Бернулли во второй части своей знаменитой книги «Ars conjectandi» («Искусство предугадывания»), опубликованной в 1713 г. Он же ввел соответствующий термин и употреблял в нашем смысле также термин «перестановка». Термин же «сочетание» применял еще Б. Паскаль.

Современная символика сочетаний была предложена разными авторами учебных руководств лишь в XIX в. В частности, знак факториала (!) был введен в 1808 г. в одном французском учебнике Хр. Крампа. Термин же «факториал» был образован от слова «фактор» (множитель), происходящего от латинского factor — производящий.

Известно, что формула

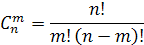
приводит к введению определений:

О том, что нуль-факториал должен быть по определению равен единице, писал еще в 1656 г. Дж. Валлис в «Арифметике бесконечных».

Во второй половине XVIII в. наметилось большое ее оживление, связи с чем даже появилось название комбинаторный анализ, однако значительных результатов достигнуто не было. Комбинаторика в известной мере способствовала развитию теории определителей, она нашла важнейшее применение в теории вероятности, параллельно с которой она развивалась в XVII—XVIII вв. В настоящее время она применяется также в некоторых вопросах теории групп и в квантовой механике.

Поиск по сайту: