АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формулы Бернулли и Пуассона

Читайте также:
  1. II. Приготовление мазка крови для подсчета лейкоцитарной формулы
  2. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  3. Аналитическая запись логической формулы КЦУ
  4. Вопрос 1 Схема Бернулли
  5. Вывод общей формулы обратной матрицы
  6. Вывод формулы Литтла
  7. Выражения. Формулы.
  8. Гироскоп.Вывод формулы частоты прецессии гироскопа.
  9. Глава 3. Мобилизующие формулы
  10. Гранична теорема Пуассона
  11. Диффузия в газах. Вязкость газов. Теплопроводность газов. Коэффициенты диффузии, вязкости, теплопроводности. Вывод формулы для коэффициента диффузии.
  12. Закон постоянства состава. Химические формулы

Схемой Бернулли будем называть схему одинаковых независимых испытаний, каждое из которых заканчивается одним из двух несовместных исходов: или наступает некоторое событие А, или оно не наступает, т. е. наступает противоположное ему событие Независимость испытаний означает, что вероятность события А в любом испытании не зависит от того, какими сведениями мы располагаем относительно результатов других испытаний. Кроме того, в схеме Бернулли предполагается, что вероятность события А в одном испытании остается постоянной во всей серии испытаний.

Многие практически важные задачи приводят к отысканию вероятности 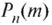того, что при n испытаниях, произведенных по схеме Бернулли, событие А произойдет m раз (m = 0, 1, 2, n), если известна вероятность р события А в каждом испытании. Справедлива следующая формула Бернулли:

Пример 1. Что вероятнее выиграть у равносильного противника:

а) три партии из четырех или пять из восьми;

б) не менее трех партий из четырех или не менее пяти партий из восьми? Решение. Так как противники равносильны, то вероятности выигрыша и проигрыша в каждой партии одинаковы.

а) вероятность выиграть три партии из четырех:

вероятность выиграть пять партий из восьми:

Так как 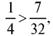то вероятнее выиграть три партии их четырех.

б) вероятность выиграть не менее трех партий из четырех:

вероятность выиграть не менее пяти партий из восьми:

Посколькуто вероятнее выиграть не менее пяти партий из

восьми.

Пример 2. Студент отвечает на 4 дополнительных вопроса при сдаче экзамена. Вероятность правильного ответа на каждый вопрос будем

считать равной Предполагая, что все ответы - события незави-

симые, найти вероятность того, что будут даны хотя бы два правильных ответа.

Решение. А = {хотя бы два правильных ответа} - это 2, 3 или 4.

Так как то - вероятность неправильного ответа

на вопрос. Эту задачу удобно решать, используя противоположные события, т. е. пользуясь равенством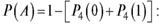

В случаях, когда в (7.15) n велико, а р мало, вместо формулы Бернулли, как правило, ограничиваются формулой Пуассона:

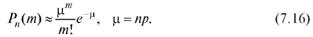
Пример 3. При перевозке 1000 стеклянных колб вероятность разбить 1 колбу равна 0,002. Какова вероятность того, что будут разбиты 4 колбы?

Решение.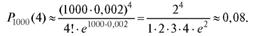


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)