 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Инструкция по выполнению практической работы
На выполнение практической работы дается 1 час 30 мин.(90 мин.). Работа состоит из 8 заданий. При их выполнении надо записать обоснованное решение. За выполнение работы выставляется оценка.
Методика анализа результатов, полученных в ходе практической работы.
Оценка тестовых заданий производится в соответствии с утвержденными критериями:
| № | Процент правильных ответов | Оценка по общепринятой шкале |
| 85-100 % | Отлично | |
| 70 – 84 % | Хорошо | |
| 50 – 69 % | Удовлетворительно | |
| 0 – 49 % | Неудовлетворительно | |
Порядок выполнения отчета по практической работе
- Прочитать методические указания.
- Решить определенный вариант.
- Ответить на контрольные вопросы.
Вариант 1
1) Установите, какие из следующих предложений являются логическими высказываниями, а какие — нет (объясните почему):
· "Солнце есть спутник Земли";
· "2+3?4";
2) Укажите, какие из высказываний предыдущего задания истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
3) Составьте таблицы истинности логического выражения:
- А Ú (B C).
4) Составьте логическую функцию F (X, Y, Z) для заданной таблицы истинности:
| X | Y | Z | F |
5) Выражение ((А) С) Ú B (C) равносильно:
а) A Ú (C);
б) (A) Ú B;
в) A Ù (C).
Вариант 2
1) Установите, какие из следующих предложений являются логическими высказываниями, а какие — нет (объясните почему):
o "сегодня отличная погода";
o "в романе Л.Н. Толстого "Война и мир" 3 432 536 слов";
2)Укажите, какие из высказываний предыдущего задания истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
3) Составьте таблицы истинности логического выражения:
o (А Ú B) (A B).
4) Составьте логическую функцию F (X, Y, Z) для заданной таблицы истинности:
| X | Y | Z | F |
5) Выражение ((А) С) Ú B (C) равносильно:
а) A Ú (C);
б) (A) Ú B;
в) A (C).
Вариант 3
1) Установите, какие из следующих предложений являются логическими
высказываниями, а какие — нет (объясните почему):
- "Санкт-Петербург расположен на Неве";
- "музыка Баха слишком сложна";
2) Укажите, какие из высказываний предыдущего задания истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
3) Составьте таблицы истинности логического выражения:
· (А Ú B) Ú (C B).
4) Составьте логическую функцию F (X, Y, Z) для заданной таблицы истинности:
| X | Y | Z | F |
5) Выражение ((А) С) Ú B (C) равносильно:
а) A Ú (C);
б) (A) Ú B;
в) A Ù (C).
Вариант 4
1) Установите, какие из следующих предложений являются логическими
высказываниями, а какие — нет (объясните почему):
- "первая космическая скорость равна 7.8 км/сек";
- "если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный".
2) Укажите, какие из высказываний предыдущего задания истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
3) Составьте таблицы истинности логического выражения:
А Ú (B C).
4) Составьте логическую функцию F (X, Y, Z) для заданной таблицы истинности:
| X | Y | Z | F |
5) Выражение ((А) С) Ú B (C) равносильно:
а) A Ú (C);
б) (A) Ú B;
в) A (C).
Вариант 5
1) Установите, какие из следующих предложений являются логическими
высказываниями, а какие — нет (объясните почему):
- "если один угол в треугольнике прямой, то треугольник будет тупоугольным";
- "железо — металл";
- "если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный".
2) Укажите, какие из высказываний предыдущего задания истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.
3) Составьте таблицы истинности логического выражения:
o (А Ú B) (A B).
4) Составьте логическую функцию F (X, Y, Z) для заданной таблицы истинности:
| X | Y | Z | F |
5) Выражение ((А) С) Ú B (C) равносильно:
а) A Ú (C);
б) (A) Ú B;
в) A (C).
Вариант 1
1. Построить закон распределения и функцию распределения числа попаданий мячом в корзину при двух бросках, если вероятность попадания равна 0,4.
2. Случайная величина Х задана функцией плотности вероятности:

Найти математическое ожидание величины Х.
Вариант 2
1. В партии из 10 деталей имеется 8 стандартных. Наугад отобраны 2 детали. Составить закон распределения стандартных деталей среди отобранных.
2. Случайная величина Х задана функцией плотности вероятности:

Найти математическое ожидание величины Х.
Вариант 3
1. В партии из 6 деталей имеется 4 стандартных. Наугад отобраны 3 детали. Составить закон распределения дискретной случайной величины Х - числа стандартных деталей среди отобранных.
2. Случайная величина Х задана функцией плотности вероятности:

Найти дисперсию Х.
Вариант 4
1. Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины Х - числа выпадений четного числа очков на обеих игральных костях.
2.. Случайная величина Х задана функцией плотности вероятности:

Найти дисперсию Х.
Вариант 5
1. В парии деталей 10 % нестандартных. Наугад отобраны 4 детали. Написать биномиальный закон распределения дискретной случайной величины Х - числа нестандартных деталей среди четырех отобранных.
2. Случайная величина Х задана функцией плотности вероятности:
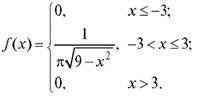
Найти дисперсию Х.
математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Х.
Вариант 1
1. Еще в XVIII веке было замечено, что среди обычной корреспонденции письма без адреса обладают определенной устойчивостью, приблизительно 25-27 на каждый миллион.
2. Студент знает 40 вопросов из 60, включенных в программу. Найти вероятность того, что студент знает 2 вопроса, содержащихся в его экзаменационном билете?
3. В одном аквариуме находятся 5 белых, 4 красных и 3 голубых рыбки. Двух случайно выбранных рыбок переносят в другой аквариум. Какова вероятность того, что обе рыбки голубые?
4. Шесть человек больны заболеванием, для которого коэффициент выздоровления составляет 98 %. Какова вероятность того, что:
а) выздоровеют все шестеро;
б) выздоровеют только пятеро?
5. В первой коробке 20 ампул, из них 18 стандартных, во второй - 10 ампул, из них 9 стандартных. Из второй коробки взята наугад ампула и переложена в первую коробку. Найти вероятность того, что случайным образом извлеченная из первой коробки ампула окажется стандартной.
Вариант 2
1. При бросании симметричной монеты вероятность выпадения герба на основании классического определения будет, очевидно, равна 0,5. Английский статистик К. Пирсон (1857-1936) бросил симметричную монету 24 000 раз, при этом герб выпал 12 012 раз, следовательно, относительная частота выпадения герба оказалась равной 0,5005, т. е. как и ожидалось, оказалась примерно равной 0,5.
2. Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал 5 различных цветов?
3. Из десяти билетов выигрышными являются два. Определить вероятность того, что среди взятых наудачу пяти билетов:
а) один выигрышный;
б) два выигрышных;
в) хотя бы один выигрышный
4. На клумбе растут 20 красных, 30 синих и 40 белых астр. Какова вероятность сорвать в темноте окрашенную астру, если срывают одну астру?
5. В первой коробке 20 ампул, из них 18 стандартных, во второй - 10 ампул, из них 9 стандартных. Из второй коробки взята наугад ампула и переложена в первую коробку. Найти вероятность того, что случайным образом извлеченная из первой коробки ампула окажется стандартной
Вариант 3
1. Некоторая вакцина эффективна на 75 % в формировании иммунитета. Вакцинировали двух человек. Пусть А и В - независимые события, состоящие в том, что соответственно первый и второй человек приобретают иммунитет. Найти вероятность того, что:
а) оба человека приобрели иммунитет;
б) первый приобрел иммунитет, а второй - нет;
в) оба не приобрели иммунитета.
2. Сколькими способами можно выбрать 3 различных краски из имеющихся 5?
3. Набирается четырехзначный номер телефона. Какова вероятность набрать его правильно с первого раза, если все цифры номера нечетные и ровно три из них пятерки?
4. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после первого отказа отвечать на вопрос преподаватель задает еще один вопрос?
5. В вычислительной лаборатории имеются 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения расчета автомат не выйдет из строя, равна 0,95, а для полуавтомата эта вероятность равна 0,8. Студент выполняет расчет на машине, выбранной наугад. Найти вероятность того, что до окончания расчета машина не выйдет из строя.
Вариант 4
1. Команда на хорошем поле выигрывает с вероятностью 2/3, а на плохом - с вероятностью 1/2. Известно, что 3/4 игр проводится на хорошем поле. Какова вероятность выиграть в выбранном наудачу матче?
2. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из 5 языков - русского, английского, французского, немецкого и итальянского - на любой другой из этих 5 языков?
3. Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наугад выбирают 5 человек на конференцию. Найти вероятности следующих событий:
• А - будут выбраны одни третьекурсники;
• В - все первокурсники попадут на конференцию;
• С - не будет выбран ни один второкурсник;
• D - выберут одного первокурсника, двоих второкурсников и двоих третьекурсников.
4. В читальном зале 6 учебников по теории вероятности, из которых 3 в переплете. Библиотекарь взял наугад 2 учебника. Найти вероятность того, что оба учебника окажутся в переплете.
5. Производится серия из 4 выстрелов по мишеням с вероятностью попадания в каждом выстреле p = 1/4. Предполагая, что результаты выстрелов - события независимые, найти вероятность того, что будут хотя бы два попадания.
Вариант 5
1. Имеются три одинаковых ящика с шарами. В первом ящике 30 белых и 20 черных шаров, во втором - 15 белых и 15 черных шаров, в третьем - 5 белых и 15 черных шаров. Какова вероятность вытащить из случайно выбранного ящика черный шар?
2. Для эксперимента по определению скорости роста требуется выбрать 4 штамма бактерий из имеющихся 8. Сколькими способами это можно сделать?
3. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором 3 вопроса.
4. В библиотеке имеются учебники по химии и биологии. Вероятность того, что любой читатель возьмет книгу по химии, равна 0,7, а по биологии - 0,3. Определить вероятность того, что 5 читателей подряд возьмут книги или только по химии, или только по биологии, если каждый берет только одну книгу.
5. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия (остальные - годные!).
Поиск по сайту: