 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Мат. ожидание дискретной случайной велечины и его свойства (включая теорему 1)
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то  .
.
Если случайная величина Х принимает счетное число значений, то  , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание дискретной случайной величины—это неслучайная величина (т.е. число, постоянная).
1.Математическое ожидание постоянной величины равно самой постоянной
M(C)=C.
Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно, 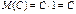 .
.
Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х.
2.множитель можно выносить за знак математического ожидания:
M(CX)=CM(X).
Если случайная величин Х имеет ряд распределения
| X | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
Ряд распределения случайной величины СХ
| СХ | Сx1 | Сx2 | … | Сxn | … |
| Р | p1 | p2 | … | pn | … |
Математическое ожидание случайной величины СХ  .
.
Случайные величины X1,X2,…,Xn называются независимыми, если для любых числовых множеств B1,B2,…,Bn 
3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий
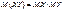 .
.
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
4.Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых:
 .
.
Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.
Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:  .
.
Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события  . По свойству 4:
. По свойству 4:
 .
.
Согласно примеру 2  . Таким образом, получим
. Таким образом, получим  .
.
Поиск по сайту: