Формулы полной вероятности и Баеса: 23 стр

Теорема 1. Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности:

, или .

Так как события образуют полную группу, то можно записать .

Событие А может произойти только с одним из событий Hi, i 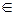{1,2,…,n}, то А=АН1+АН2+…+АНn. По теореме сложения вероятностей

Замечание: при применении формулы полной вероятности события Н1,Н2,…,Нn, образующие полную группу, называются гипотезами.

Теорема 2. Пусть события Н1, Н2, …, Нn образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса:

,

Замечание. При применении формулы Байеса вероятности называются априорными вероятностями гипотез. Вероятности P(H1|A),…,P(Hn|A) называют апостериорными вероятностями гипотез.

4)схема независимых испытаний Бернули. Полиномиальное распределение:

Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы называем успехом и неудачей.

, , p+q=1.

Предположим, что мы производим независимо друг от друга n таких испытаний.

Последовательность n испытаний называется испытаниями Бернулли, если эти испытания

независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию.

Элементарным исходом будет являться:

(w1,w2,…,wn), .

Всего таких исходов 2n.

(1)

Формула (1) показывает, что события независимы.

Обозначим через µ число успехов в n испытаниях Бернулли. — вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие .

По теореме сложения получим

Таким образом, получим

—формула Бернулли.

Предположим, что в результате испытания возможны k исходов E1, E2, …, Ek,

P(Ei)=pi, . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле:

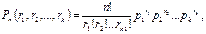где

Эта формула полиномиальное распределения, обобщающая формулу Бернулли.

Поиск по сайту: