Случайные велечины, функция распределения и её свойства

Случайной величиной Х называется функция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R.

Множество значений случайной величины обозначается Ωх. Одной из важных характеристик случайной величины является функция распределения случайной величины.

Функцией распределения случайной величины Х называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.

.

.

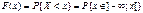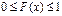Если рассматривать Х как случайную точку на оси ох, то F(x) с геометрической точки зрения—это вероятность того, что случайная точка Х в результате реализации эксперимента попадет левее точки х.

Свойства функции распределения.

1.Функция распределения F(x)–неубывающая функция, т.е. для 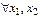таких что x1<x2 .

Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е. , представим в виде объединения двух несовместимых событий

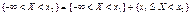
Тогда по теореме сложения вероятностей получим

, т.е.

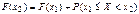. Поскольку , то .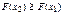

2.Для любых

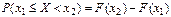
Замечание. Если функция распределения F(x) непрерывная, то свойство выполняется и при замене знаков ≤ и < на < и ≤.

3.

, .

, .

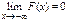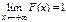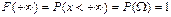4.Функция F(x) непрерывна слева. (т.е. ).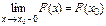

5. Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.

.

Достоверное событие {-∞<x<+∞} представим в виде двух несовместимых событий. . Найдем их вероятности

.

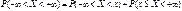Поскольку вероятность достоверного события равна единице, то

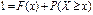.Отсюда .

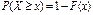Поиск по сайту: