ЛЕКЦИЯ №5

8.5. Непрерывные случайные величины (НСВ). Плотность вероятности.

Выше дано понятие НСВ, имеющей бесконечное несчетное множество значений. Приведем более строгое определение.

Определение 26. СВ Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Теорема 11. Вероятность любого отдельно взятого значения НСВ равно нулю.

Замечание 10. На первый взгляд данное утверждение может показаться парадоксальным. Действительно, если событие имеет ненулевую вероятность, то оказывается, что оно является суммой событий, состоящих в принятии СВ Х любых конкретных значений на отрезке и имеющих нулевую вероятность. Но никакого противоречия здесь нет, т.к. теорема сложения справедлива только для конечного или счетного множества событий, а НСВ таковым не является.

Представление о событии, имеющем ненулевую вероятность, но складывающуюся из событий с нулевой вероятностью, не более парадоксально, чем представление об отрезке, имеющем определенную длину, тогда как все точки отрезка имеют длину, равную нулю.

Следствие.

Задание НСВ с помощью функции распределения не является единственным. Введем понятие плотности вероятности НСВ.

Определение 27. Плотностью вероятности непрерывной случайной величины Х называется производная ее функции распределения: .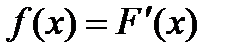

Плотность вероятности , как и функция распределения , является одной из форм закона распределения, но в отличие от функции распределения, она существует только для НСВ. Плотность вероятности иногда называют дифференциальной функцией распределения. График называют кривой распределения.

Свойства .

1º. .

2º. .

3º. .

4º. .

Геометрически свойства 1 и 4 означают, что кривая распределения лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс равна единице.

8.6. Числовые характеристики НСВ.

Понятие математического ожидания и дисперсии, введенные выше для ДСВ, можно распространить на НСВ. Заменяя в соответствующих формулах (8.1) и (8.2) знак суммирования на знак интеграла с бесконечными пределами интегрирования, скачущий аргумент - непрерывно меняющимся , а вероятности - функцией распределения , получим формулы для математического ожидания и дисперсии НСВ Х:

(8.5)

(8.6)

Все свойства и , рассмотренные выше для ДСВ, справедливы и для НСВ.

Замечание 11. На практике при вычислении дисперсии удобнее пользоваться не формулой (8.6), а формулой, полученной из этой с использованием свойств математического ожидания:

. (8.7)

Пример 8.7. Функция задана в виде:

=

Найти:

1) значение а, при котором функция будет плотностью вероятности некоторой СВ Х;

2) функцию распределения ;

3) ;

4) числовые характеристики СВ Х.

Решение. 1) Для вычисления а используем свойство 4 плотности вероятности:

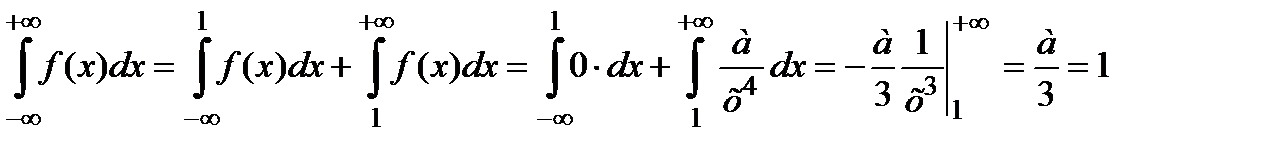откуда .

2) найдем по свойству 3 плотности вероятности.

Если , то .

Если , то .

Таким образом, =

3) По свойству 2 плотности вероятности

= .

Замечание 12. можно найти и по свойству 3 :

= .

4) Найдем числовые характеристики по формулам (8.5) и (8.7).

.

.

Поиск по сайту: