АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задачи для домашнего задания №7

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Ситуационные задачи и тестовые задания.
  3. II. Основные задачи и функции
  4. II. Расчетная часть задания
  5. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  6. II. Цель и задачи государственной политики в области развития инновационной системы
  7. III. Задания для самостоятельной работы по изучаемой теме.
  8. III. Задания для самостоятельной работы по изучаемой теме.
  9. III. Задания для самостоятельной работы по изучаемой теме.
  10. III. Задания для самостоятельной работы по изучаемой теме.
  11. III. Задания для самостоятельной работы по изучаемой теме.
  12. III. Задания для самостоятельной работы по изучаемой теме.

1. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего деления. Считая, что ошибки измерения распределены равномерно а) записать плотность распределения ; б) записать функцию распределения ; в) найти математическое ожидание 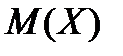и дисперсию с помощью , а также используя формулы для равномерного распределения; г) найти вероятность того, что при отсчете будет сделана ошибка, меньшая 0,04.

2. Время ремонта и обслуживания автомобиля после поездки случайно и имеет показательный закон распределения с дисперсией 25мин2. а) Записать плотность распределения ; б) записать функцию распределения ; в) найти среднее время ремонта и обслуживания автомобиля; г) найти вероятность того, что после очередной поездки время обслуживания не превысит 10 минут.

3. Случайная величина - годовая процентная ставка потребительского кредита – подчинена закону нормального распределения с параметрами и . а) Записать плотность распределения ; б) найти вероятность того, что в текущем году процентная ставка не превысит 15,5%; в) найти доверительный интервал , в котором с вероятностью 0,9544 будет находиться годовая процентная ставка.

 

ОТВЕТЫ

1. а) ; б) ;

в) , ; г) 0,4. 4. а) ;

б) ; в) мин; г) 0,8647.

5. при ; б) 0,9772; в) (8,5;15,5).


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)