 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ТЕСТ №2
| Задание 1 | |||||||||||
 и и 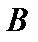 - независимые события. Тогда справедливо следующее утверждение: - независимые события. Тогда справедливо следующее утверждение:
| 1) 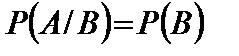 2)
2)  3)
3) 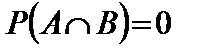 4)
4) 
| ||||||||||
| Задание 2 | |||||||||||
| Вероятность невозможного события равна… | 1)  2)
2) 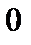 3)
3)  4)
4) 
| ||||||||||
| Задание 3 | |||||||||||
| Количество шестизначных четных чисел, которые можно составить из цифр 1, 3, 4, 5, 7 и 9, если в каждом из этих чисел ни одна из цифр не повторяется, равно… | 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||
| Задание 4 | |||||||||||
| Бросают одновременно две игральные кости. Тогда вероятность того, что сумма выпавших очков не больше 6, равна… | 1) 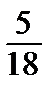 2)
2) 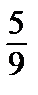 3)
3)  4)
4) 
| ||||||||||
| Задание 5 | |||||||||||
| Каждая буква слова «РЕМЕСЛО» написана на отдельной карточке, затем карточки перемешаны. Вынимают три карточки наугад. Вероятность получить слово «ЛЕС» равна… | 11) 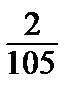 2)
2)  3)
3) 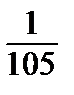 4)
4) 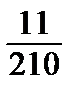
| ||||||||||
| Задание 6 | |||||||||||
Вероятность появления каждого из двух независимых событий  и и 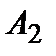 соответственно равны 0,6 и 0,5. Тогда вероятность появления только одного из них равна… соответственно равны 0,6 и 0,5. Тогда вероятность появления только одного из них равна…
| 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||
| Задание 7 | |||||||||||
| В лаборатории имеется шесть новых и четыре старых компьютера. Вероятность безотказной работы нового компьютера равна 0,95, а старого – 0,8. Производится расчет на наудачу выбранной машине. Вероятность того, что во время работы машина не выйдет из строя равна… | 1)  2)
2) 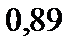 3)
3)  4)
4) 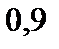
| ||||||||||
| Задание 8 | |||||||||||
| В магазин вошли 6 покупателей. Вероятность совершить покупку для каждого вошедшего одна и та же и равна 0,2. Вероятность того, что 3 из них совершат покупку равна… | 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||
| Задание 9 | |||||||||||
Дискретная случайная величина  задана законом распределения вероятностей задана законом распределения вероятностей
Тогда дисперсия случайное величины | 1) 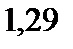 2)
2)  3)
3) 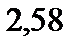 4)
4) 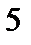
| ||||||||||
| Задание 10 | |||||||||||
Дана функция
 .
Эта функция является плотностью распределения некоторой непрерывной случайной величины .
Эта функция является плотностью распределения некоторой непрерывной случайной величины  при при  равном… равном…
| 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||
| Задание 11 | |||||||||||
Непрерывная случайная величина  равномерно распределена на отрезке равномерно распределена на отрезке  .Тогда математическое ожидание этой равномерно распределенной случайной величины равно… .Тогда математическое ожидание этой равномерно распределенной случайной величины равно…
| 1)  2)
2) 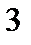 3)
3)  4)
4) 
| ||||||||||
| Задание 12 | |||||||||||
Из генеральной совокупности извлечена выборка объема 
Тогда | 1)  2)
2)  3)
3)  4)
4) 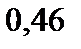
| ||||||||||
| Задание 13 | |||||||||||
| Мода вариационного ряда 1, 2, 3, 4, 5, 5,7 равна… | 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||
| Задание 14 | |||||||||||
Статистическое распределение выборки имеет вид
Тогда объем выборки равен… | 1)  2)
2)  3)
3) 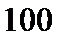 4)
4) 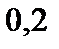
| ||||||||||
| Задание 15 | |||||||||||
Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза… , то конкурирующей может быть гипотеза…
| 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||
| Задание 16 | |||||||||||
Точечная оценка математического ожидания нормального распределения равна  . Тогда его интервальная оценка может иметь вид… . Тогда его интервальная оценка может иметь вид…
| 1) 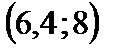 2)
2)  3)
3)  4)
4) 
| ||||||||||
| Задание 17 | |||||||||||
| Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 5, 6, 9, 10, 12. Тогда несмещенная оценка математического ожидания равна… | 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||
| Задание 18 | |||||||||||
Дана выборка объема 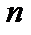 . Если каждый элемент выборки увеличить на 5 единиц, то выборочная дисперсия . Если каждый элемент выборки увеличить на 5 единиц, то выборочная дисперсия  … …
| 1) не изменится 2) увеличится на 5 единиц 3) увеличится на 10 единиц 4) уменьшиться на 5 единиц |
ОТВЕТЫ
| Тест №1 | Тест №2 | ||
| Задание | Ответ | Задание | Ответ |
Поиск по сайту:


 равна…
равна…


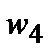 равен…
равен…