Основные законы распределения

В данном параграфе рассмотрим основные законы распределения дискретных и непрерывных случайных величин, используемых для построения теоретико-вероятностных моделей реальных технико-экономических явлений.

Для дискретных распределений укажем следующие основные позиции:

1) определение;

2) ряд распределения;

3) формулы для вычисления числовых характеристик.

4) область применения.

9.1. Биномиальный закон распределения.

1) Определение 28. ДСВ Х имеет биномиальный закон распределения с параметрами и , если она принимает значения 0, 1, …, , …, с вероятностями

(9.1)

где , .

2) Ряд распределения биномиального закона имеет вид:

	0			…		…
				…		…

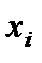
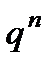
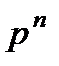
3) , ,

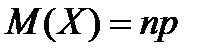4) Биномиальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и других областях.

9.2. Равномерный закон распределения (для ДСВ).

1) Определение 29. ДСВ Х имеет равномерный закон распределения, если она принимает значений с равными вероятностями = .

2)Ряд распределения равномерного закона имеет вид:

		…
		…

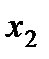
3) , , .

Заметим, что матожидание является просто средним арифметическим значений случайной величины, а формула для вычисления дисперсии довольно громоздка, легче считать по формуле из свойства 4 дисперсии.

9.3. Закон распределения Пуассона.

1) Определение 30. ДСВ Х имеет закон распределения Пуассона с положительным параметром , если она принимает значения 0, 1, …, , … (бесконечное, но счетное множество значений) с вероятностями

. (9.2)

2) Ряд распределения закона Пуассона имеет вид:

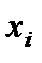
	0			…		…
				…		…

3) , , .

4) По закону Пуассона распределены число рождений четверней, число сбоев на автоматической линии, число отказов сложной системы, число требований на обслуживание, поступивших в единицу времени в систему массового обслуживания и др.

9.4. Геометрическое распределение.

1) Определение 31. ДСВ Х имеет геометрическое распределение с параметром , если она принимает значения 0, 1, …, , … (бесконечное, но счетное множество значений) с вероятностями

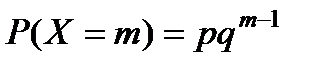, (9.3)

где , .

2) Ряд геометрического распределения имеет вид:

				…		…
				…		…

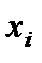
ДСВ Х, имеющая геометрическое распределение, представляет собой число испытаний, проведенных по схеме Бернулли, с вероятностью наступления события в каждом испытании до первого положительного исхода.

3) , .

9.5. Гипергеометрическое распределение.

1) Определение 32. ДСВ Х имеет гипергеометрическое распределение с параметрами n, M, N, если она принимает значения 0, 1, 2, …, m, …, min(n, M) c вероятностями

, (9.4)

где 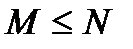, , 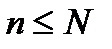- натуральные числа.

3) , . (9.5)

4) Гипергеометрическое распределение широко используется в практике статистического приемочного контроля качества промышленной продукции, в задачах, связанных с организацией выборочного обследования и др.

Теперь разберем основные законы распределения НСВ. Для непрерывных распределений укажем следующие основные позиции:

1) определение и плотность вероятности ;

2) функцию распределения ;

3) графики этих функций;

4) вероятность попадания в интервал ;

5) формулы для вычисления числовых характеристик;

6) область применения.

9.6. Равномерный закон распределения.

1) Определение 33. НСВ Х имеет равномерный закон распределения на отрезке [ a; b ], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне него, т.е.

=

2) Функция распределения СВ Х, распределенной по равномерному закону, есть

=

3) Кривая распределения и график функции распределения приведены на рис. 3(а,б).

а)

б)

Рис.3.

4) ;

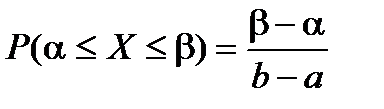5) ; .

6) Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчиненном этому закону.

9.7. Показательный (экспоненциальный) закон распределения.

1) Определение 34. НСВ Х имеет показательный закон распределения с параметром , если ее плотность вероятности имеет вид:

=

2) Функция распределения СВ Х, распределенной по показательному закону, есть

=

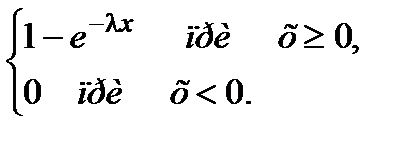
3) Кривая распределения и график функции распределения приведены на рис.4.

Рис.4

4 )

5) , , .

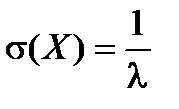6) Показательный закон распределения играет большую роль в теории надежности и теории массового обслуживания.

9.8. Нормальный закон распределения.

Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Этот факт доказан в теореме Ляпунова, понятие о которой мы сформулируем позже.

1) Определение 35. НСВ Х имеет нормальный закон распределения (закон Гаусса) с параметрами и , если ее плотность вероятности имеет вид:

= (9.6)

Термин «нормальный» не совсем удачный. Многие признаки подчиняются нормальному закону, например, рост человека, дальность полета снаряда и т.п. Но если какой-либо признак подчиняется другому закону распределения, то это вовсе не говорит о «ненормальности» явления, связанного с этим признаком.

2) Функция распределения СВ Х, распределенной по нормальному закону, есть

= , (9.7)

где - интегральная функция Лапласа.

3) Кривая распределения и график функции распределения приведены на рис.5 (а, б).

а)

б)

Рис.5.

4 ) 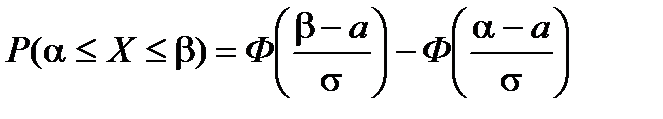(9.8)

5) Математическое ожидание СВ Х, распределенной по нормальному закону, равно параметру этого закона, а дисперсия – параметру , т.е.

М(Х)= , D(X)= .

При изучении нормального закона, в силу его исключительности, немного отступим от нашего плана, заявленного перед п.9.6.

6) Вероятность отклонения нормально распределенной СВ от ее математического ожидания вычисляется по формуле:

. (9.9)

7) Правило «трех сигм». Хотя при нормальном распределении СВ. Х 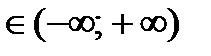, практически все значения СВ находятся в интервале . Докажем этот факт. По формуле (9.9)

.

Вывод: если известно, что практически всегда нормально распределенная СВ Х принимает значения из некоторого конечного интервала, то , а середина этого интервала есть параметр .

Замечание 13. Понятие о теореме Ляпунова.

Если имеется очень большое количества линейно-независимых НСВ и каждая из них ничтожно мало влияет на другие и имеет ограниченное математического ожидание и дисперсию, то распределение суммы всех этих величин стремится к нормальному, если количество всех этих величин стремится к бесконечности.

Пример 9.1. Полагая, что рост взрослых мужчин есть нормально распределенная СВ Х с параметрами =173 и =36, найти:

1) выражение плотности вероятности и функции распределения ;

2) долю костюмов 4-го роста (176-182 см) и 3-го роста (170-176 см), которые нужно предусмотреть в общем объеме производства.

Решение. 1) По формулам (9.6) и (9.7) запишем

=

= .

2) Найдем вероятности попадания в интервалы (176-182 см) и (170-176 см) по формуле (9.8)

.

Вывод: костюмы 4-го роста должны занимать в производстве примерно 24%, 3-го роста – 38%.

Поиск по сайту: