Введение. Первые вероятностные задачи появились из практики азартных игр, причем, их решением занимались известные математики

Первые вероятностные задачи появились из практики азартных игр, причем, их решением занимались известные математики. Решим простую задачку. Бросают три игральные кости. Что вероятнее: получить в сумме выпавших очков 11 или 12? Существует следующая легенда: однажды к Галилею за консультацией обратился рыцарь именно с таким вопросом. Он заявил Галилею, что согласно логике, обе эти суммы должны появляться одинаково часто, но опыт учит другому, что сумма 11 появляется чаще, чем 12. Почему? Обоснование рыцаря на первый взгляд звучит убедительно: числа 11 и 12 могут быть разложены на сумму трех слагаемых лишь шестью способами:

11=1+5+5=1+4+6=2+3+6=2+4+5=3+3+5= 3+4+4;

12=1+5+6=2+4+6=2+5+5=3+4+5=3+3+6=4+4+4;

отсюда, по его мнению, вытекает равновозможность обоих событий.

Однако Галилей возразил ему, сказав, что каждое из этих разложений следует снабдить еще определенным весом, и пояснил свою мысль таким рассуждением. Назовем кости «первой», «второй» и «третьей»; тогда разложение 1+5+5 на самом деле может произойти не одним, а тремя различными способами:

1+5+5=5+1+5=5+5+1,

т.е., единица может выпасть на первой, второй или третьей кости. Точно также разложение 1+4+6 может произойти шестью различными способами:

1+4+6=1+6+4=4+1+6=4+6+1=6+1+4=6+4+1.

Таким образом, 11 в сумме может появиться не шестью, а 27 различными равновозможными способами. Сумма же 12, оказывается, разлагается лишь 25 различными способами. Дело в том, что разложение 4+4+4 осуществимо лишь одним способом. Позже посчитаем вероятности выпадения этих сумм.

Есть гораздо более важные проблемы, которые приходится решать в практической деятельности. Сколько дорожных происшествий произойдет завтра в городе? Сколько вызовов от больных поступит в скорую помощь? Сколько лет проживет только что родившийся ребенок? Как много времени придется затратить на поиск неисправности в сложном техническом устройстве? Все эти вопросы обладают одной особенностью – на них невозможно дать однозначного ответа, поскольку процессы с ними связанные лишены полной определенности. Во всех подобных случаях мы говорим, что интересующее нас событие является случайным.

Со случайными явлениями мы вынуждены сталкиваться постоянно, и, зачастую, именно они определяют структуру интересующего нас процесса. Так, при организации работы телефонной станции, необходимо учитывать, что моменты поступления вызовов от абонентов и длительность разговоров случайны. В грузовой морской порт суда дальнего плавания прибывают не точно по расписанию, а в моменты времени, сильно отличающиеся от запланированного и время обработки судна (погрузочно-разгрузочные работы) зависят от многих факторов и не может быть точно определено заранее. Случайные события играют большую роль, как в научных исследованиях, так и в практической деятельности. Более того, при проектировании ответственных сооружений мы должны опираться на эти случайные явления. Это обстоятельство привело к тому, что за последние три столетия случайные явления были подвергнуты систематическому исследованию.

Теория вероятностей – это раздел математики, изучающий закономерности массовых случайных явлений. Объект изучения – математическая модель случайного явления. Метод изучения – формальная математическая логика.

§2. События, их классификация.

Теория вероятностей занимается изучением не любых событий, которые в житейской практике называются случайными, а только тех из них, которые обладают определенными свойствами:

1) события могут быть осуществлены, в принципе, неограниченное число раз, причем, в неизменных условиях;

2) события должны обладать статистической устойчивостью.

Подчеркнем, что теория вероятностей не занимается изучением уникальных явлений, которые не допускают повторений.

Дадим основные определения:

Определение 1. Испытанием называется комплекс некоторых условий, которые можно осуществлять неограниченное число раз.

Определение 2. Событием называется некоторый исход испытания.

Определение 3. Событие называется достоверным, если в результате испытания оно обязательно произойдет.

Например, при подбрасывании игральной кости выпадет число не более шести.

Определение 4. Событие называется невозможным, если в результате испытания оно не может произойти.

Например, при подбрасывании игральной кости выпадет число 8.

Определение 5. Событие, которое в результате данного испытания может произойти, а может и не произойти, называется случайным.

Например, при подбрасывании игральной кости выпадет число 3.

Определение 6. Совместными называются два события, из которых одно не исключает другого, т.е. они могут произойти оба в одном испытании.

Например, события: А - занять первое место в соревновании по бегу, В – побить мировой рекорд в соревновании по бегу являются совместными.

Определение 7. Несовместными называются два события, которые не могут произойти оба в одном испытании.

Например, события: - получить «5» на экзамене по теории вероятностей в ближайшую сессию, – получить «3» на экзамене по теории вероятностей в ближайшую сессию, являются несовместными.

Определение 8. Полной группой событий называется множество событий несовместных между собой, и таких, что одно из них обязательно произойдет.

Полная группа событий обозначается так: { А, В, С } – события А, В, С образуют полную группу.

Определение 9. Противоположными называются два события, одно из которых приходит тогда и только тогда, когда не происходит другого.

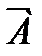Событие, противоположное событию , обозначается так: . Противоположные события образуют полную группу, т.е.

Например, события: А – попасть в мишень и – промахнуться, являются противоположными, т.е. В= .

Поиск по сайту: