 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачи для домашнего задания №6
1. Закон распределения ДСВ задан таблицей
| X | -5 | |||
| p | 0,3 | 0,4 | 0,2 | 0,1 |
Найти  ,
,  и
и 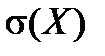 . Построить функцию распределения
. Построить функцию распределения  . Вычислить
. Вычислить  и
и  .
.
2. Среди 7 купленных театральных билетов 3 билета в партер. Наудачу взяли 4 билета. Составить ряд распределения числа билетов в партер среди выбранных. Построить график функции распределения.
3. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок в среднем в 20% случаев. Составить закон распределения числа возвращенных в срок кредитов из 3 выданных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение с помощью ряда распределения и по формулам биномиального распределения.
4. Экзаменатор задает студенту вопросы, пока тот правильно отвечает, затем ставит оценку. Максимальное количество заданных вопросов – четыре. Вероятность правильного ответа на один вопрос равна 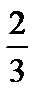 . Построить многоугольник распределения числа заданных студенту вопросов.
. Построить многоугольник распределения числа заданных студенту вопросов.
5.  - число появлений события А в 8 независимых испытаниях. Вероятность наступления события А в каждом испытании одна и та же. Известно, что
- число появлений события А в 8 независимых испытаниях. Вероятность наступления события А в каждом испытании одна и та же. Известно, что 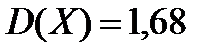 . Найти
. Найти  .
.
6. Монета подбрасывается несколько раз. Какое количество раз надо бросить монету. Чтобы математическое ожидание числа появлений герба было равно 25? Чему будет равна дисперсия для этой случайной величины?
7. Найти математическое ожидание случайной величины 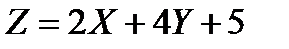 , если известны математические ожидания
, если известны математические ожидания  и
и 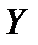 :
: 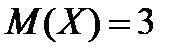 ,
,  .
.
8. Даны законы распределения двух независимых случайных величин:
| X | ||||||||
| p | 0,4 | 0,2 | 0,1 | 0,3 | ||||
| Y | ||||||||
| p | 0,5 | 0,2 | 0,3 | |||||
Найти математическое ожидание и дисперсию случайной величины  .
.
9. Найти  и
и  для задачи №1 домашнего задания №6 с помощи ряда распределения и сделать проверку, используя формулы для данного биномиального распределения.
для задачи №1 домашнего задания №6 с помощи ряда распределения и сделать проверку, используя формулы для данного биномиального распределения.
10. Может ли случайная величина  иметь биномиальное распределение, если: а)
иметь биномиальное распределение, если: а) 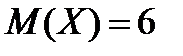 ,
, 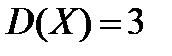 ; б)
; б)  ,
,  .
.
ОТВЕТЫ
1. 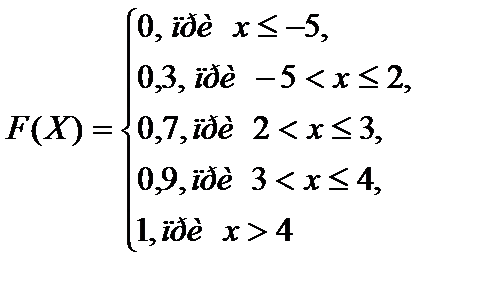 ,
, 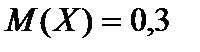 ,
, 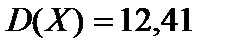 ,
,  .
. 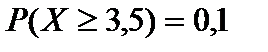 и
и 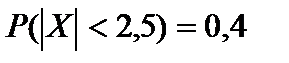 .
.
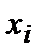
| ||||
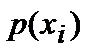
| 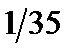
| 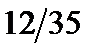
| 
| 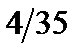
|
2.

2. 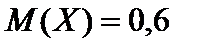 ,
, 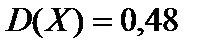 ,
, 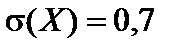 . 3. Отметить точки (
. 3. Отметить точки (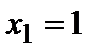 ,
, 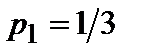 ), (
), (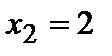 ,
, 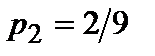 ), (
), (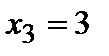 ,
, 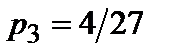 ), (
), (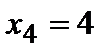 ,
, 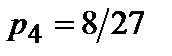 ) и соединить ломаной. 4.
) и соединить ломаной. 4.  или
или 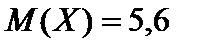 . 5.
. 5. 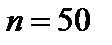 ,
,  . 6.
. 6. 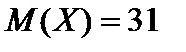 . 7.
. 7. 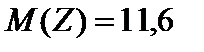 ,
, 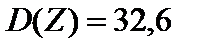 . 8.
. 8. 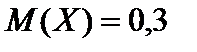 ,
,  . 9. а) да.
. 9. а) да.  ,
,  ; б) нет, т.к.
; б) нет, т.к.  не может быть не целым.
не может быть не целым.
Поиск по сайту: