Повторные независимые испытания

7.1. Схема повторных испытаний. Формула Бернулли. Наивероятнейшее число наступлений события.

Схема повторных испытаний служит базовой моделью для решения большого числа практических задач.

Определение 15. Испытания называются независимыми, если результат прошлых испытаний не может влиять на результат следующих испытаний, т.е. на вероятность наступления события в следующих испытаниях.

Определение 16. Испытания проводятся по схеме Бернулли, если:

1) испытания независимы;

2) в результате испытания возможны только два исхода: событие А или ему противоположное ;

3) вероятность наступления события А постоянна во всех испытаниях.

Теорема 7.(Формула Бернулли). Если испытания проводятся по схеме Бернулли, то вероятность того, что в n испытаниях событие А наступит m раз вычисляется по формуле

,

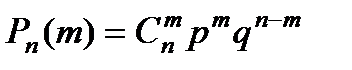где - вероятность наступления события А в одном испытании, 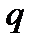= 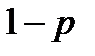- вероятность наступления события .

Пример 7.1. Какова вероятность того, что при10 бросаниях игральной кости два раза выпадут три очка?

Решение. Здесь , , 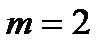, и

.

Замечание 3. При больших n вычисление факториала ведется приближенно с очень большой погрешностью, т.к. функция n! растет очень быстро (20!≈2,4·10¹⁸).

Вывод: Хотя формула Бернулли верна при любых n, но на практике ей можно пользоваться только при .

Определение 17. Число т₀ наступлений события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события по крайней мере не меньше, вероятности других событий при любом т₀.

Наивероятнейшее число т₀ определяем из двойного неравенства

.

Отметим, что так как разность , то всегда существует целое число т₀, удовлетворяющее данному неравенству. При этом если - целое число, то наивероятнейших чисел два: 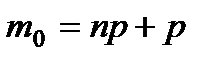и .

Пример 7.2. В примере 7.1 найдем наивероятнейшее число выпадений тройки.

Решение. ,

,

.

7.2. Формула Пуассона.

На практике мы часто встречаемся с ситуациями, когда число испытаний n исчисляется сотнями и тысячами, а вероятность очень мала (или весьма близка к 1). Это так называемые «редкие события», особенно часто встречающиеся в теории массового обслуживания.

Пример 7.3. При транспортировке изделие может быть повреждено с вероятностью 0,002. Найти вероятность того, что в партии из 2000 изделий в пути окажутся поврежденными три изделия.

Решение. Здесь 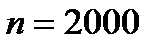, , , Пользуясь формулой Бернулли, запишем

.

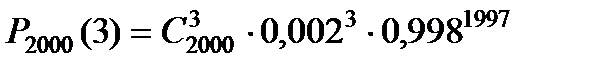Совершенно ясно, что формула здесь непригодна, т.к. вычислить число сочетаний и последующие степени – занятие весьма трудоемкое. И здесь нам на помощь приходит приближенная формула Пуассона, в основе которой лежит следующая теорема.

Теорема 8. Если

1) испытания проводятся по схеме Бернулли;

2) n→∞, →0,

то вероятность того, что в n испытаниях событие А наступит m раз вычисляется по формуле

, где .

Вернемся к примеру 7.2. Решим его, используя формулу Пуассона: , .

Замечание 4. Погрешность приближения в данном случае незначительна – всего 0,05%, т.к. выполнены условия теоремы: мало, n велико. Если эти условия не соблюдать, то погрешность получится ощутимой: при n =50 и =0,08 ошибка приближения будет уже 2,02%, а при n =20 и =0,2 ошибка уже будет 5,12%.

7.3. Локальная и интегральная теоремы Муавра-Лапласа.

Если при больших значениях n вероятность существенно отличается от нуля, то параметр λ становится значительным по величине и вычисление вероятности по формуле Пуассона тоже будет сопряжено с большими трудностями. В таком случае пользуемся другой приближенной формулой, которая является содержанием следующей теоремы.

Теорема 9.(Локальная теорема Муавра-Лапласа). Пусть испытания проводятся по схеме Бернулли. Тогда вероятность того, что в n испытаниях событие А появится ровно m раз при n→∞ приближенно равна

,

где , - функция Гаусса.

Скажем несколько слов о функции Гаусса. Она табулирована (см. Приложение, табл. 1) Аргумент х может принимать любые действительные значения. Сама функция – четная, поэтому таблица составлена только для положительных значений аргумента.

Вывод: чтобы найти вероятность m появлений события А в n испытаниях (когда n велико, а существенно отличается от нуля и единицы), необходимо по известным значениям m, n, и вычислить х, по таблице 1 Приложений найти и вычислить по приближенной формуле

.

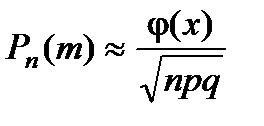Пример 7.4. Процент заболеваемости рыб в вырастном хозяйстве равен 20%. Определить вероятность того, что среди 2000 случайно отобранных особей 380 окажутся больными.

Решение. В денном случае =0,2, n=2000, m=380, =0,8.

Вычисляем: .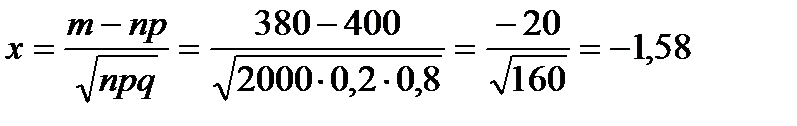

Из табл.1 Приложений находим: . Тогда .

Замечание 5. При большом числе испытаний вероятности настолько малы, что им соответствующие события вряд ли могут представлять практический интерес. В подобных ситуациях вопрос обычно ставится о вероятности того, что число появлений m события А заключено в некотором интервале, т.е. о вероятности . Решение этого вопроса связано с интегральной теоремой Муавра-Лапласа.

Теорема 10. (Интегральная теорема Муавра-Лапласа). Пусть испытания проводятся по схеме Бернулли. Тогда вероятность того, что в n испытаниях (при n→∞) событие А появится не менее и не более раз приближенно равна

,

где 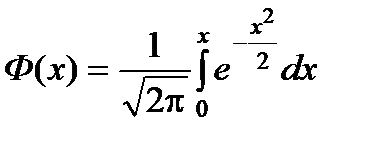- функция Лапласа, , .

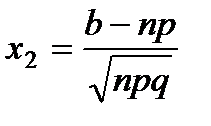Отметим несколько важных свойств функции Лапласа:

1) функция нечетная, т.е. ;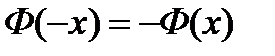

2) функция табулирована, в силу нечетности только для положительных значений аргумента (см. табл.2 Приложений);

3) если , .

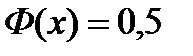Пример 7.5. В условиях предыдущей задачи (пример 7.4) найти вероятность того, что среди 2000 случайно отобранных рыб больными окажутся от 380 до 430 особей.

Решение. Вычисляем и :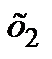

, .

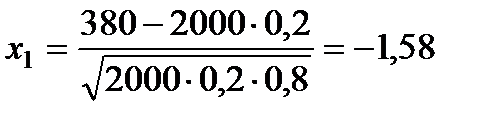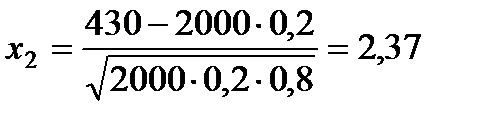Из табл.2 Приложений находим:

, .

Значит,

Поиск по сайту: