 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема 1 о достаточных условиях существования экстремума
Пусть функция  непрерывна в некотором интервале, содержащем критическую точку первого рода
непрерывна в некотором интервале, содержащем критическую точку первого рода  и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки
и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки  Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при
Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при  функция имеет максимум. Если же при переходе через точку
функция имеет максимум. Если же при переходе через точку  слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
Таким образом, если 
то в точке  функция имеет максимум;
функция имеет максимум;
если 
то в точке  функция имеет минимум.
функция имеет минимум.
При этом надо иметь ввиду, что условия  должны выполняться для всех значений
должны выполняться для всех значений  достаточно близких к
достаточно близких к  т.е. во всех точках некоторой достаточно малой окрестности критической точки
т.е. во всех точках некоторой достаточно малой окрестности критической точки 
Доказательство. Предположим сначала, что производная меняет знак с плюса на минус, т.е. выполняются условия  Применяя теорему Лагранжа к разности
Применяя теорему Лагранжа к разности  получим
получим
 где ξ есть точка, лежащая между
где ξ есть точка, лежащая между 
1) Пусть  тогда
тогда 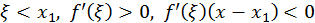 и, следовательно,
и, следовательно, 
2) Пусть  тогда
тогда  и, следовательно,
и, следовательно, 
(1) и (2) показывают, что для всех значений  достаточно близких к
достаточно близких к  значения функции меньше, чем значения функции в точке
значения функции меньше, чем значения функции в точке  Следовательно, в точке
Следовательно, в точке  функция
функция  имеет максимум.
имеет максимум.
Аналогичным образом доказывается вторая часть теоремы о достаточных условиях минимума.
 Проиллюстрируем смысл теоремы 1 на рисунке. В точке
Проиллюстрируем смысл теоремы 1 на рисунке. В точке  и для
и для  достаточно близких к
достаточно близких к  выполняется условие
выполняется условие 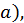 значит в точке
значит в точке  - максимум. В точке
- максимум. В точке 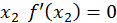 и для
и для  достаточно близких к
достаточно близких к  выполняется условие
выполняется условие  значит в точке
значит в точке  - минимум. В точке
- минимум. В точке 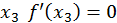 и для всех значений
и для всех значений  достаточно близких к
достаточно близких к  выполняются неравенства
выполняются неравенства
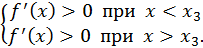
Значит функция возрастает как при 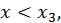 так и при
так и при 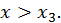 Следовательно, при
Следовательно, при  функция не имеет ни максимума, ни минимума.
функция не имеет ни максимума, ни минимума.
Поиск по сайту: