Непрерывность функции нескольких переменных

Функция называется непрерывной в точке 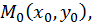если она

1) определена в точке 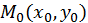и в некоторой ее окрестности,

2) существует предел

3) этот предел равен частному значению

Условие непрерывности функции 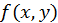в точке 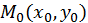символически может быть выражено так:

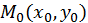причем точка стремится к точке произвольным образом, оставаясь в области определения функции.

Если обозначим то равенство можно переписать так:

или

Обозначим

При и 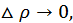и обратно,

если 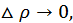то и

Замечая далее, что выражение, стоящее в квадратных скобках в равенстве есть полное приращение функции равенство можно переписать в форме:

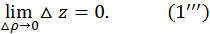
Это условие непрерывности функции 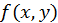в точке 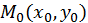в разностной форме.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области.

Теорема. Если функция определена и непрерывна в замкнутой области, то она ограничена и достигает своего наименьшего и наибольшего значений (без доказательства).

Если в некоторой точке не выполняется хотя бы одно из трех условий непрерывности функции в точке, то точка называется точкой разрыва функции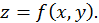

Функция двух переменных может иметь не только точки разрыва, но и линии разрыва. Например, для функции любая точка параболы является точкой разрыва. Говорят, что данная функция имеет линию разрыва.

Аналогично, говорят, что функция трех переменных 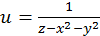имеет поверхность разрыва – параболоид вращения

Поиск по сайту: