Теорема Лагранжа о конечных приращениях

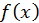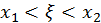Если – дифференцируемая функция на некотором промежутке и - любые значения из этого промежутка, то где (1)

Доказательство. На графике функции проведем секущую АВ через точк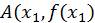и и Будем перемещать эту секущую параллельно начальному положению до тех пор, пока она не превратится в касательную 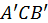к графику нашей функции в некоторой точке его где Согласно нашему построению угловой коэффициент секущей равен угловому коэффициенту касательной поэтому откуда получается (1).

Следствие 1. Если производная функции равна нулю на некотором промежутке, то функция есть тождественная постоянная на этом промежутке.

Пусть при 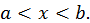Полагая в (1) , где 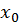– некоторое фиксированное значение из и где – любое значение из этого интервала, будем иметь

. Отсюда 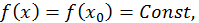если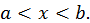

Следствие 2. Если две функции имеют равные производные на некотором промежутке, то эти функции на рассматриваемом промежутке отличаются друг от друга самое большее на постоянное слагаемое.

Пусть 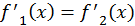при Тогда на этом промежутке имеем Следовательно, в силу следствия 1 функция для всех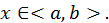

Поиск по сайту: