АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные свойства неопределенного интеграла

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  3. I.3. Основные этапы исторического развития римского права
  4. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  5. II. Основные задачи и функции
  6. II. Основные показатели деятельности лечебно-профилактических учреждений
  7. II. Основные проблемы, вызовы и риски. SWOT-анализ Республики Карелия
  8. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  9. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  10. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  11. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  12. V2: Электрические и магнитные свойства вещества

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е. если то и

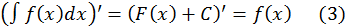
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

Это следует из (3).

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

Справедливость проверяется дифференцированием.

В формулах (4) и (5) знак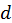и и , следующие друг за другом в том или другом порядке, взаимно уничтожают друг друга (если не учитывать постоянного слагаемого). В этом смысле дифференцирование и интегрирование и являются взаимно обратными математическими операциями.

4. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов

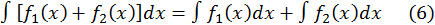
Для доказательства найдем производные от левой и правой частей этого равенства и убедимся, что они равны между собой. Следовательно, левая часть от правой может отличаться лишь на постоянное слагаемое. В этом смысле и надо понимать равенство (6).

5. Постоянный множитель можно выносить за знак интеграла

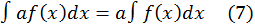
Найдем производные от левой и правой частей и увидим, что они равны. Следовательно, левая часть от правой может отличаться лишь на постоянное слагаемое.

Таблица неопределенных интегралов

Непосредственно из определения и таблицы производных вытекает таблица интегралов.

1.

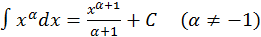
2.

3.

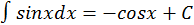
4.

5.

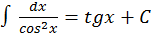
6.

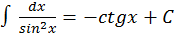
7.

8. f9.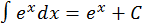

10.

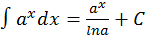
11.

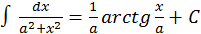
12.

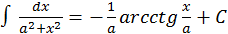
13.

14.

15.

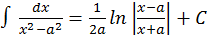
16. .


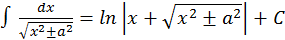1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)