Частные производные функции нескольких переменных

Частной производной по от функции называется предел отношения частного приращения 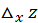к приращению при стремлении к нулю.

Частная производная по от функции 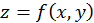обозначается одним из символов:

Таким образом, по определению,

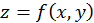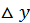Аналогично частная производная по от функции определяется как предел отношения частного приращения функции к приращению при стремлении 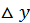к нулю. Частная производная по обозначается одним из символов:

Заметив, что 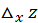вычисляется при неизменном 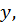а при неизменном мы можем определения частных производных сформулировать по-другому.

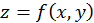Частной производной по от функции называется производная по вычисленная в предположении, что постоянная.

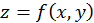Частной производной по от функции называется производная по 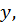вычисленная в предположении, что постоянная.

Из этого определения ясно, что правила вычисления частных производных совпадают с правилами, указанными для функций одного переменного, и только требуется каждый раз помнить, по какому переменному ищется производная.

Пример 1.

Пример 2.

Частные производные функции любого числа переменных определяются аналогично.

Пример 3.

Геометрический смысл частных производных функции двух переменных 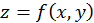состоит в следующем (смотрите соответствующий рисунок в предыдущей лекции):

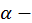где угол между осью и касательной в точке к линии пересечения поверхности 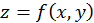и плоскости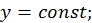

где угол между осью и касательной в точке к линии пересечения поверхности 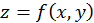и плоскости

Поиск по сайту: