Функции нескольких переменных

Полный дифференциал 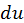функции от нескольких переменных есть в свою очередь функция тех же переменных, и мы можем определить полный дифференциал этой последней функции. Таким образом мы получим дифференциал второго порядка первоначальной функции который также будет функцией тех же переменных, а его полный дифференциал приведет нас к дифференциалу третьего порядка первоначальной функции и т.д.

Рассмотрим подробнее случай функции двух переменных и будем предполагать, что переменные и являются независимыми переменными.

По определению:

При вычислении будем принимать во внимание, что дифференциалы 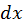и независимых переменных надо рассматривать как величины постоянные, а потому их можно выносить за знак дифференциала.

Вычисляя точно так же мы получим:

Эти выражения и приводят нас к следующей символической формуле для дифференциала любого порядка:

причем формулу эту надо понимать так: сумму, стоящую в круглых скобках, надо возвысить в степень 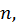применяя формулу бинома Ньютона, после чего показатели степеней у и надо считать указателями порядка производных по и от функции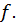

Формула обобщается без труда и на случай функции любого числа независимых переменных.

В приведенных выше рассуждениях мы предполагали, что значения дифференциалов 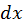и постоянны. Это предположение может быть выполнено в случае, когда аргументы и функции 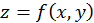являются независимыми переменными. Если же аргументы и представляют собой дифференцируемые функции каких-либо других переменных, то выражение дифференциала при отличается, вообще говоря, от его выражения в форме Убедимся в этом на примере дифференциала второго порядка для функции 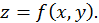Пусть, например, В силу инвариантности формы первого дифференциала имеем:

Найдем в этом общем случае.

При вычислении и мы уже не имеем права выносить 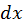и за знак дифференциала, как это делали выше, но должны применять формулу для дифференциала произведения. Мы получим, таким образом,

Сумма первых двух слагаемых в правой части этого равенства даст нам выражение, которое мы имели выше для и окончательно получим:

то есть в рассматриваемом общем случае выражение для будет содержать добавочные слагаемые, зависящие от и

Поиск по сайту: