АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема Ролля о корнях производной

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Внешние эффекты (экстерналии). Теорема Коуза.
  3. Внешние эффекты трансакционные издержки. Теорема Коуза
  4. Внешние эффекты, их виды и последствия. Теорема Коуза
  5. Внешние эффекты. Теорема Коуза.
  6. Внешние эффекты. Теорема Коуза.
  7. Вопрос 1 теорема сложения вероятностей
  8. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  9. Вопрос. Теорема Котельникова (Найквиста)
  10. Вопрос: Производная сложной функции. Производные и дифференциалы высших порядков. Теорема Ролля, Лагранжа, Коши.
  11. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  12. Вычисление производной по двум точкам

Между двумя последовательными корнями дифференцируемой функции всегда содержится по меньшей мере один корень ее производной.

Доказательство. Если - дифференцируемая функция и 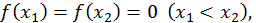то из формулы (1) имеем

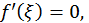или так как то где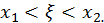

Замечание 1. Теорема имеет простую геометрическую интерпретацию. Между точками найдется по меньшей мере одна точка, в которой касательная к графику функции параллельна оси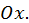

Замечание 2. Теорему можно сформулировать и в более общем виде.

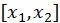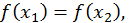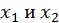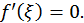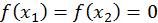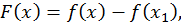Если - функция, дифференцируемая на и то между найдется точка ξ, в которой производная равна нулю, то есть Действительно, случай рассмотрен выше; если то введем функцию тогда 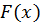дифференцируема и 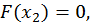т.е. для функции 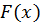выполнены условия теоремы Ролля. Следовательно, существует точка ξ такая, что а значит и


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 |

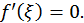
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)