Вычисление производной по двум точкам

Первая производная наиболее просто вычисляется при аппроксимации функции f (x) прямой линией. В этом случае касательная к кривой в одной точке заменяется секущей, проходящей через две точки кривой. Для точки х₁ производная может быть рассчитана по формулам:

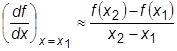, (28.3)

или

. (28.4)

Эти формулы равноправны, хотя могут привести к различным результатам, как это показано на рис.28.2. Если интервалы x ₂- x ₁ и х ₁- х ₀ равны, то более точной будет формула

. (28.5)

При расчетах по неравномерной сетке можно вычислить производные по формулам (28.3) и (28.4), а затем усреднить их с учетом весовых коэффициентов:

.

Логично предположить, что ближе к истинному значению производной будет значение, рассчитанное по формуле, у которой меньше интервал дифференцирования. Сумма весовых коэффициентов должна быть равна единице. Из этих соображений получаем весовые коэффициенты:

для первой формулы ,

для второй формулы .

Окончательно формула для вычисления производной принимает вид

. (28.6)

При x ₂- x ₁= х ₁- х ₀ она сводится к формуле (28.5).

Также можно аппроксимировать функцию f (x) степенным многочленом, например, многочленом второй степени:

.

Коэффициенты а ₀, а ₁, а ₂ рассчитываются по формулам:

Дифференцируя многочлен, получаем

При x = х ₁ эта формула сводится к выражению

. (28.7)

Для равноотстоящих узлов, когда x ₂- x ₁= х ₁- х ₀= h, получаем

. (28.8)

Аппроксимируя функцию f (x) многочленом более высокой степени, можно получить соответствующие формулы для вычисления производных по 4, 5 и более точкам.

Поиск по сайту: