АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

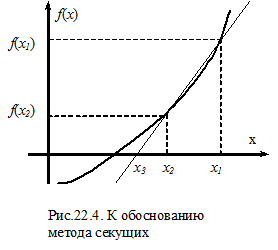
Схожесть и различие метода касательных и секущих решения нелинейных уравнений

Читайте также:
  1. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  2. II. Проблема источника и метода познания.
  3. MathCad: способы решения системы уравнений.
  4. SWOT-анализ в качестве универсального метода анализа.
  5. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  6. Административными методами можно предотвратить необоснованные расходы (хищение, злоупотребление).
  7. Алгоритм метода ветвей и границ
  8. Алгоритм проведения таксонометрического метода
  9. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
  10. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
  11. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  12. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ

В методе Ньютона необходимо вычислять производные . Это может потребовать много времени, может оказаться трудным или даже невозможным делом, особенно если вычисление включает, например, вычисление интеграла, решение дифференциального уравнения или если значение функции определяется результатом работы некоторого физического устройства.

Значение производной можно вычислить приблизительно по значениям функции в двух точках x1 и x2, как это показано на рис.22.4.

Заменив в формуле (22.1.) производную ее приближенным значением

,

По сравнению с методом Ньютона из-за погрешности в определении производной для нахождения корня требуется выполнить большее количество шагов. Однако в методе секущих на каждом шаге вычисляется только одно значение функции, в то время как в методе Ньютона вычисляются значения функции и ее производной, поэтому скорость счета у них приблизительно одинакова. Недостаток метода секущих связан с тем, что в знаменателе формулы (22.2) стоит разность значений функции. Вдали от корня это несущественно, но вблизи от корня значения функции малы и очень близки. В результате этого возникает потеря значащих цифр, приводящая к «разболтке» счета, когда результаты вычисления начинают колебаться около истинного значения, не сходясь к нему. Это ограничивает точность счета.

Следует отметить еще одну сторону метода секущих. Формула (22.2) идентична формуле метода хорд:

.

Однако, метод касательных не требует указания диапазона изменения знака функции и при этом обеспечивает обычно большую скорость расчета, чем метод хорд. В свою очередь, метод хорд гарантирует нахождения корня и исключает возможность появления «разболтки», так как корень всегда находится внутри диапазона неопределенности и длина диапазона сокращается на каждом шаге.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (1.1 сек.)