Метод касательных (Ньютона) решения нелинейных уравнений

Этот метод также называется методом касательных или методом линеаризации. Если функция f (x) в области определения имеет непрерывную производную , значения которой легко вычисляются, то можно значительно ускорить процесс приближения к корню.

На рис.22.1. показана схема итерационных вычислений корня уравнения по методу Ньютона. Для начала расчета должны быть заданы начальная точка x₀ и допустимая погрешность e. В точке x₀ вычисляются значения функции f (x) и ее производной . Далее функция f (x) аппроксимируется ее производной, новое приближение к корню определяется как точка пересечения касательной с осью абсцисс. Значение производной в точке x₀ равно

,

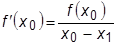откуда находится координата точки x₁:

.

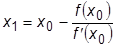Поскольку за один ход не удается найти корень уравнения, то процесс повторяется, новые приближения определяются по рекуррентной формуле

(22.1)

до тех пор, пока не будет выполнено условие или .

Блок-схема метода Ньютона приведена на рис. 22.2. Если нулевое приближение выбрано достаточно близко к корню, то скорость сходимости велика. К достоинствам этого метода следует отнести также то, что для начала расчета не требуется указывать диапазон, на котором функция меняет знак, а достаточно выбрать только начальную точку.

Допустим, необходимо вычислить квадратный корень из числа a, то есть решить уравнение . Запишем его в виде . Тогда .

Согласно (2.4) получим формулу

,

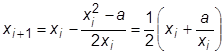которая позволяет вычислить квадратный корень, используя только операции сложения и деления. Именно эта формула запрограммирована в карманных калькуляторах.

К недостаткам метода следует отнести возможность расхождения, то есть возникновения ситуации, когда метод не в состоянии найти корни.

При 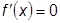метод не определен, при малых или неудачном начальном приближении могут возникнуть проблемы со сходимостью, когда последующее приближение хуже предыдущего. Подобный случай показан на рис. 22.3.

Поиск по сайту: