АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вычисление определенных интегралов методом Симпсона

Читайте также:
  1. Абсолютная и условная сходимость несобственных интегралов.
  2. Адаптивные программы вычисления определенных интегралов
  3. Алгоритм решения ЗЛП графическим методом
  4. Алгоритм решения систем линейных уравнений методом Жордана-Гаусса
  5. Анализ движения денежных средств прямым и косвенным методом
  6. Анализ методом деревьев событий и отказов
  7. Б) Вычисление тригонометрических функций.
  8. В определенных условиях ВЗД способны обеспечить ощутимую экономию.
  9. Векторное и смешанное произведение векторов. Свойства и геометрический смысл. Вычисление через координаты векторов.
  10. Вибір оптимального варіанта СМ методом мікровартостей
  11. Визначення осмотичного тиску клітинного соку плазмолітичним методом
  12. Визначення параметрів емпіричної формули за методом найменших квадратів.

Возьмем для аппроксимации функции f (x) многочлен второй степени . Чтобы определить коэффициенты a,b,c, необходимо на интервале аппроксимации задать три точки. Выберем шаг интегрирования D x и вычислим значения функции на концах интервала и в его середине. Обозначим, как это показано на рис.23.5, значения аргумента через x0, x1, x2 и, соответственно, значения функции через f0, f1, f2. Половину шага интегрирования обозначим .

Уравнение параболы, проходящей через три точки, можно записать в виде

.

Учитывая, что , при интегрировании этой функции в пределах от x0 до x0+2h после преобразований получим:

.

Для всего интервала интегрирования будем иметь:

 

, (23.5)

где .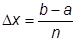

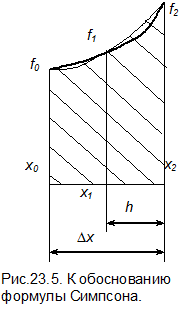
Это формула Симпсона.

Как и для рассмотренных ранее методов, вычисления интегралов по формуле Симпсона могут быть по блок-схемам рис.23.2 или рис.23.3.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)